Permutations and Combinations


Permutations and Combinations
Permutations

When you have to take a smaller group of items from a larger group, you often need to know how many different ways there are of making a selection (this comes in handy when studying probability).

In some situations, the order of the items in the smaller group is important.  For example, the diagram below shows all possible results for the top three dogs at a dog show:

Each arrangement lists the same dogs, but the order of first-, second-, and third-place winners differ.  Arrangements such as these are called permutations.  A permutation is an arrangement is which order is important.  You can use the counting principle to count permutations.

Counting Permutations
 
Example 1

You have just downloaded 5 new songs.  You can use the counting principle to count the different permutations of those 5 songs.  This is the number of different sequences in which you can listen to the new songs on your playlist.



You can listen to the songs in 120 different orders.

Factorials!
 
In the last example, you evaluated 5 × 4 × 3 × 2 × 1.  When you multiply a number by the number 1 less than itself, then by the number 1 less than that, and so on, all the way down to 1, this is known as a factorial.  You can write "5 × 4 × 3 × 2 × 1" as "5!" which is read as "5 factorial."

5!  =  5 × 4 × 3 × 2 × 1
n!  =  n × (n − 1) × (n − 2) × ... × 1

Note:  The value of 0! is defined as 1.


Example 2

Twelve marching bands entered a competition.  In how many different ways can first, second, and third places be awarded?



There are 1,320 different ways to award the three places.


Permutation Notation

The previous example shows how to find the number of permutations of 12 items taken 3 at a time.  We can write this as 12P3.  In general, the permutation formula is defined as follows:

The number of permutations of n objects taken r at a time = nPr =

Example: 

***

Combinations

In permutations, the order in which something is arranged is important. 

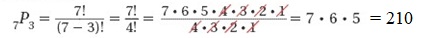
A combination, on the other hand, is a group of items whose order is not important. For example, suppose you go to lunch with a friend. You choose milk, soup, and a salad. Your friend chooses soup, a salad, and milk. The order in which the items are chosen does not matter. You both have same meal.


Listing Combinations


Example 

You have 4 tickets to the county fair and can take 3 of your friends. You can choose from Abby (A), Brian (B), Chloe (C), and David (D). How many different choices of groups of friends do you have?


Solution

List all possible arrangements of three friends. Then cross out any duplicate groupings that represent the same group of friends.

You have 4 different choices of groups to take to the fair.


Combination Notation 

In Example 1, after you cross out the duplicate groupings, you are left with the number of combinations of 4 items chosen 3 at a time. Using notation, this is written 4C3.


To find the number of combinations of n objects taken r at a time, divide the number of permutations of n objects taken r at a time by r !.

Formula:                        Example: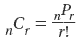 
                   


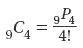
Evaluating Combinations 

Find the number of combinations if you select 3 items from a group of 8.


8C3



Find the number of combinations if you select 7 items from a group of 9.

9C7



Distinguishing Permutations and Combinations

Examples

State whether the possibilities can be counted using a permutation or combination. Then write an expression for the number of possibilities. 

a. There are 8 swimmers in the 400 meter freestyle race. In how many ways can the swimmers finish first, second, and third? 

Solution: Because the swimmers can finish first, second, or third, order is important. So the possibilities can be counted by evaluating 8P3. 


b. Your track team has 6 runners available for the 4-person relay event. How many different 4-person teams can be chosen? 

Solution: Order is not important in choosing the team members, so the possibilities can be counted by evaluating 6C4.