Parts of a Circle
Parts of a Circle
A circle is a set of all points in a plane that are all an equal distance from a single point, the center. The distance from a circle's center to a point on the circle is called the radius of the circle. A radius is a line segment with one endpoint at the center of the circle and the other endpoint on the circle. For the circle below, AD, DB, and DC are radii of a circle with center D.
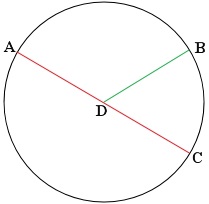
A line segment that crosses the circle by passing through its center is called a diameter. The diameter is twice the length of the radius. In the circle above, AC is a diameter of the circle.
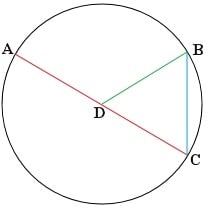
A chord is a segment that also has endpoints on the circle, but does not need to cross through the center. On the circle below, BC and AC are chords. A diameter is a chord that passes through the center of the circle.
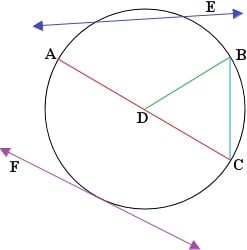
A secant is a line that intersects with a circle at two different points. In the circle below, line E is a secant. A tangent is a line that intersects with the circle at only one point. In the circle below, line F is a tangent.
Tangents
If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency.
Example
Jason is located at a point P, 28 feet from the edge of a circular garden. The distance from Jason to a point of tangency on the garden is 56 feet. What is the radius of the garden?
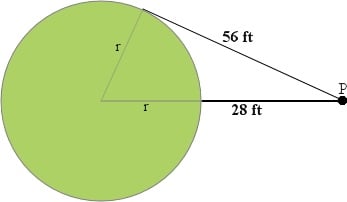
(r + 28)2 = r2 + 562
r2 + 56r + 784 = r2 + 3136
r2 + 56r − r2 = 3136 − 784
56r = 2352
r = 42
Arcs
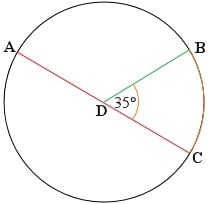
An angle whose vertex is on the center of a circle is called a central angle. In the circle below, ∠ADB is a central angle. If the measure of ∠ADB is less than 180°, then the interior of ∠ADB forms the minor arc while the exterior forms the major arc. The measure of an arc is defined by the measure of its central angle. In the example below, the measure of arc BC is 35o.
Chords of Circles
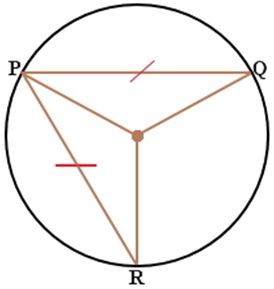
In the same circle, two minor arcs are congruent if and only if their corresponding chords are congruent. Therefore the point P shown below is called the midpoint, and arc PQ ≅ arc PR if and only if PQ ≅ PR.
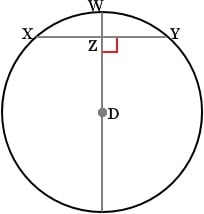
If the diameter of a circle is perpendicular to a chord, then the diameter bisects the chord and its arc. Therefore, XZ ≅ ZY when arc XW ≅ arc WY. If one chord is a perpendicular bisector of another chord, then the first chord is a diameter.
Inscribed Angle
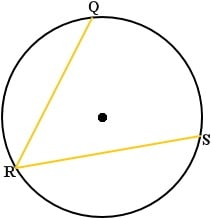
If an angle is inscribed in a circle, then its measure is half the measure of its intercepted arc. In the circle below, the measure of ∠QRS is 1/2 of the measure of arc QS.
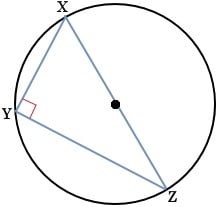
If a right triangle is inscribed in a circle, then the hypotenuse is a diameter of the circle. Conversely, if one side of an inscribed triangle is a diameter of the circle, then the triangle is a right triangle and the angle opposite the diameter is the right angle. In the circle below, ∠Y is a right angle if and only if XZ is a diameter of the circle.
A quadrilateral can be inscribed in a circle if and only if its opposite angles are supplementary. In the quadrilateral below, points P, Q, R, and S all lie on the circle if and only if m∠P + m∠R = 180o and m∠Q + m∠S = 180o.
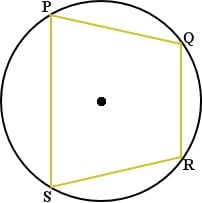
A quadrilateral that can be inscribed in a circle is known as a cyclic quadrilateral.