Transformations: Translations, Rotations, and Reflections
 Learning Target: I can identify types of geometric transformations in the plane and types of symmetry present in a figure.
Learning Target: I can identify types of geometric transformations in the plane and types of symmetry present in a figure.
Transformations
Understanding the concepts of simple geometric transformations — translations, rotations, and reflections will help you work through some of the math questions.
A translation moves a shape without any rotation or reflection. For example, the square on the left has been translated 2 units up (that is, in the positive y-direction) to get the square on the right.
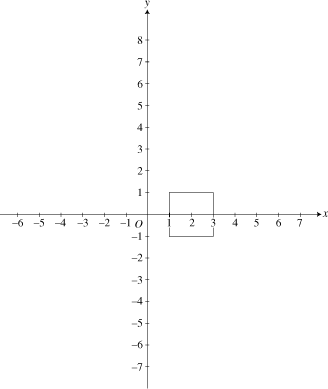
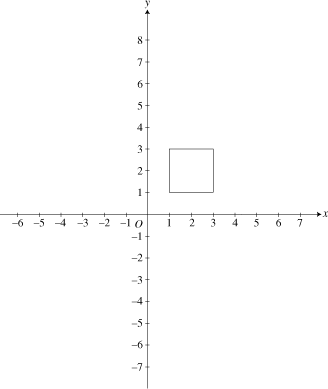
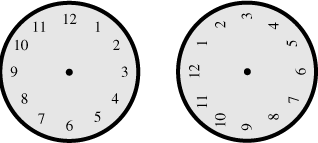
Rotating an object means turning it around a point, which is called the center of rotation. For example, when the clock face on the left is rotated 90 counterclockwise, the result is the clock face on the right:
counterclockwise, the result is the clock face on the right:
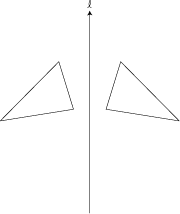
To reflect an object means to produce its mirror image with respect to a line, which is called the line of reflection. The figure below shows a triangle reflected across the line l. A mirror image is produced on the other side of the line.
If you reflect a figure twice across the same line, you get back the original figure.
Symmetry
Look at the figure below to review the concept of symmetry:
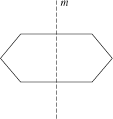
The dashed line m divides the hexagon into two halves. If the left half is reflected across line m, the result is the right half- and vice versa. In other words, if you reflect the hexagon across line m, the result is the same hexagon. The hexagon is said to be symmetrical about the line m, and m is called a line of symmetry for the hexagon.
A geometric figure may have more than one line of symmetry (for example, a rectangle), or it may have no lines of symmetry.
There is another type of symmetry. Look at the rectangle below, with point P at its center.

If you rotate the rectangle 180 (clockwise or counterclockwise) around P, then the result is the same rectangle. The rectangle is said to be symmetric around the point P, and P is called a point of symmetry for the rectangle.
(clockwise or counterclockwise) around P, then the result is the same rectangle. The rectangle is said to be symmetric around the point P, and P is called a point of symmetry for the rectangle.
Note that symmetry about a line and symmetry about a point are different properties. A given figure may have either type of symmetry and not the other, or it may have both types of symmetry (for example, a circle) or neither type.
Let's Practice Together
1.) Identify the type of transformation displayed.
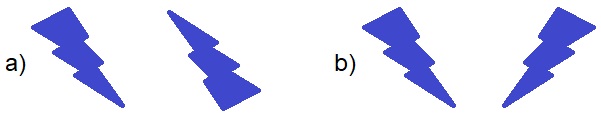
Your Turn
For each of the illustrations below, identify the type of transformation displayed.
2.)
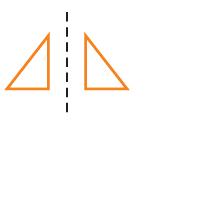
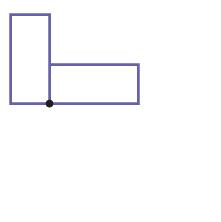
3.)
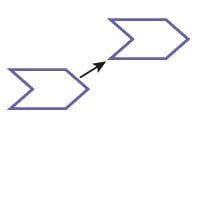
4.)
Determine whether the following shapes have line symmetry, point symmetry, or both.
5.)
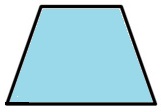
6.)
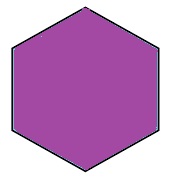
7.)
8.)

Check for Understanding
1.) Which of the following social media icons has point symmetry, but not line symmetry?

Answers
1.) a) rotation b) reflection
2.) reflection
3.) rotation
4.) translation
5.) point symmetry
6.) line symmetry
7.) point and line symmetry
8.) point and line symmetry
Check for Understanding
1.) B