Logarithmic Functions
Logarithmic Functions
Logarithmic Functions
Logarithmic functions, or logs, are the inverse of exponential functions. The two can be written in either form.
y = bx can be rewritten as logb(y) = x
The main thing to remember about log functions is that they produce exponents.
EXAMPLES
Evaluate log2 32.
The question here is basically, "What exponent of 2 will give you 32?" Remembering that 25 = 32, it follows that log2 32 = 5.
Evaluate log3 9.
Don't be fooled here. This is not a division problem; the question is asking for an exponent. Since 32 = 9, this means log3 9 = 2.
Evaluate log5 (1/25).
Remembering that negative exponents make reciprocals, we find that 5-2 = 1/25. So log5 (1/25) = -2.
Evaluate log7 (-49).
There is no such exponent that satisfies 7? = -49. Therefore, log7 (-49) does not exist.
Using the definition of logarithm, you can also solve equations.
EXAMPLE
Solve: log2(x) = 4
Understand:
This reads "the log base two of a number equals four." Solve by converting the logarithmic statement into its equivalent exponential form.
Solution:
log2(x) = 4
24 = x
16 = x
You can also get the graph of a log function from the graph of an exponential function.
Recall how y = 2x looks on the graph:
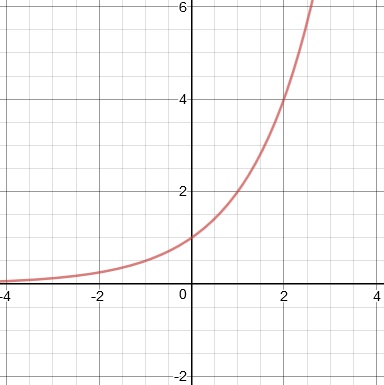
The domain is all real numbers, the range is only the positive numbers, there's a y-intercept at 1, and there's a horizontal asymptote through y = 0.
If we think about reflecting this graph over the diagonal line y = x, we get the graph of y = log2(x).
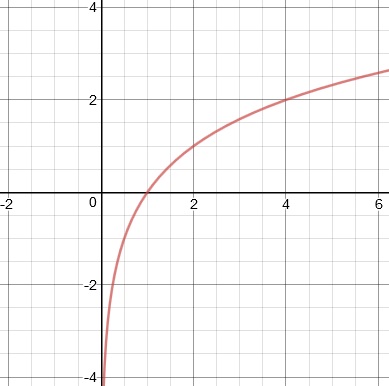
Notice with this function, the domain is only the positive numbers (remember how log7 (-49) didn't exist?), the range is all real numbers, there's an x-intercept at 1, and there's a vertical asymptote through x = 0.
Like with exponential functions, the appearance of the log function graph varies depending on the base, but all log graphs have the same general shape:
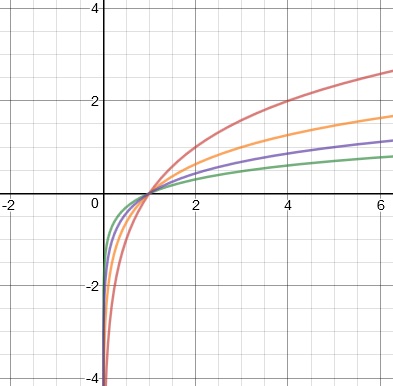
y = log2 (x)
y = log3 (x)
y = log5 (x)
y = log10 (x)
The base 10 logarithm is also known as the common logarithm. If the base isn't written, it's understood to be 10.
log (x) = log10 (x)
Practice
1. Evaluate the following, if possible: a) log4 64 b) log2 (−16) c) log3 (1/27)
2. Evaluate the following, if possible: a) log9 3 b) log7 1 c) log 100
Answers
1. a) 3 b) not possible c) −3
2. a) 1/2 b) 0 c) 2