Conic Sections
Conic Sections
Each conic section has its own typical shape and equation as shown below.
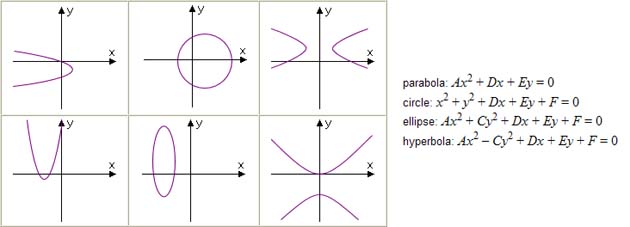
Graphing
It is helpful to recognize which type of conic section your equation represents before graphing. For each particular curve, slightly different steps may apply. In general, to graph a conic section:
1. Rewrite the equation in standard form.
2. Plot the center or vertex (h, k).
3. Locate the endpoints of the major and minor axes and/or foci.
4. Connect the endpoints of axes with a smooth curve.
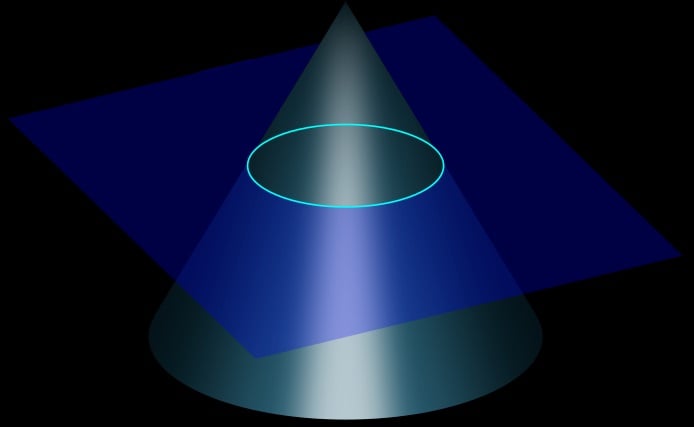
These shapes are known as "conic sections" because they can be produced by intersecting a cone with a plane in various ways. Here is a brief overview of the four major types of conic sections.
Circle
If you intersect a cone with a plane so that the plane is parallel to the base, you get a circle.
A circle is defined as the set of all points whose distance from a fixed point (the center) is always the same.
You use circles in navigation. If you're looking for something "within a 10-mile radius," you're looking inside a circle with radius 10 miles whose center is wherever you are at the moment.
Ellipse
If you intersect a cone with a plane at a slight angle to the base, you get an ellipse.
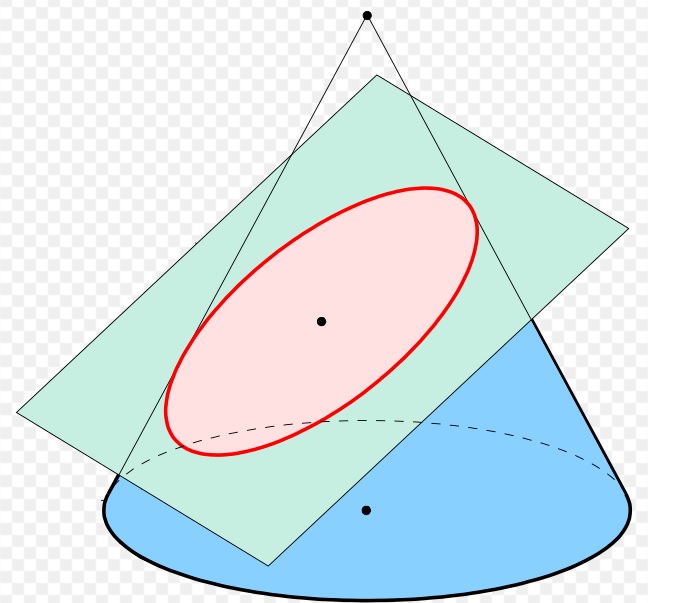
An ellipse is defined as the set of all points whose total distance from two fixed points (the foci) is always the same.
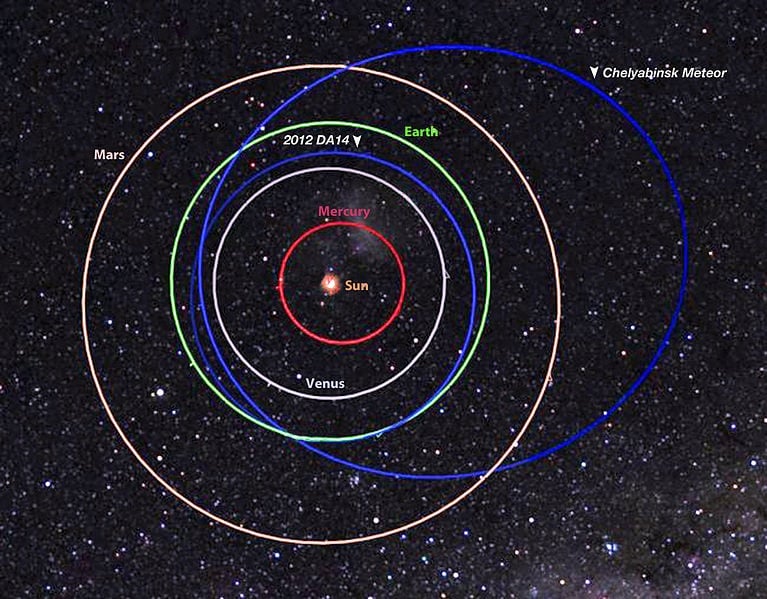
The orbits of planets, comets, and meteors are in the shape of ellipses. For such orbits in the solar system, the sun is one of the foci.
Parabolas
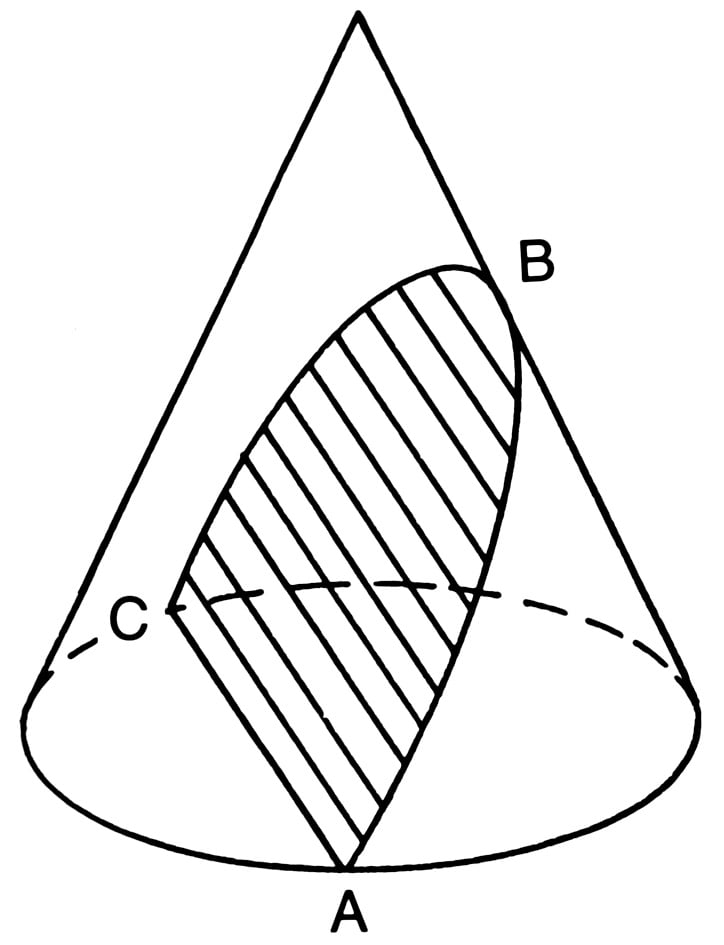
If you intersect a cone with a plane so that the plane is parallel to an edge, you get a parabola.
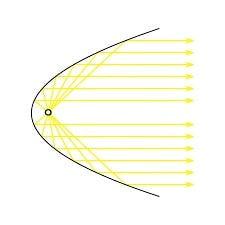
A parabola is defined as the set of points that are equidistant from a fixed point (the focus) and a fixed line (the directrix).
A parabola is used to direct light. When a light bulb is placed at the focus of a parabolic reflector, the light is sent outward in a straight line, as seen with flashlights and car headlights.
Hyperbolas
If you intersect a cone with a plane so that the plane is perpendicular to the base, you get a hyperbola.

Typically, a hyperbola is seen as two symmetrical branches, which can be generated if we include an inverted second cone on top of the first.

A hyperbola is defined as the set of points for which the difference between their distances from two fixed points (the foci) is always the same.
Security mirrors are often hyperbolic in shape. Its reflective property allows a viewer to see a wide area from where he or she is standing.
