Series
When a function is only defined for the natural numbers (1, 2, 3, 4, 5, ...), we can call the set of function values a sequence. For example, the function an = 3n - 2 leads to the sequence {1, 4, 7, 10, 13, ...} when n takes on the value of each successive natural number.
A series is the value you get when you add up all the terms of a sequence. This value is called the sum. It is denoted by the capital Greek letter, sigma: ∑
For example, to show the summation of the first ten terms of a sequence {an}, the symbol notation would be as follows:
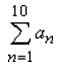
where n = 1 is the lower index, corresponding to the first term, and 10 is the upper index, corresponding to the last term. The an stands for the terms to be added. The notation is described as "the sum as n goes from one to ten of a-sub-n" and can be expanded as follows:
a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9 + a10
With an arithmetic series, a series based on an arithmetic sequence, you can find the sum quickly by using this formula:
Notice how f(1) and f(N) represent the first and last terms respectively.
Example: Find the sum 1 + 3 + 5 + 7 + ... + 99.
This is an arithmetic series because the numbers increase by the same amount each time. There are 50 numbers in this sequence (since it's exactly half as many numbers as there are from 1 to 100), so according to the formula, we have S = 50/2(1 + 99) = 25(100) = 2500.
With a geometric series, a series based on a geometric sequence, you can find the sum by using this formula:
Example: Find the sum 3 + 6 + 12 + 24 + ... + 1536.
This is a geometric series because the numbers increase by the same factor each time. In this case, the factor, or common ratio, is 2. The value of a is the first term in the series, which is 3. If you can't figure out right away how many terms there are in the series, do some reverse-engineering on the last term:
ar n-1 = 1536
3(2n-1) = 1536
2n-1 = 512
2n-1 = 29
n - 1 = 9
n = 10
There are 10 terms in the series. Now that we know N = 10, we can use the formula:
3(1 - 210) ÷ (1 - 2) = 3069
If a geometric series has a common ratio r that satisfies |r| < 1, you can find the sum of the entire series:
Example: Find the sum 50 + 10 + 2 + 2/5 + ...
This is a geometric series with an infinite number of terms, but notice that the common ratio here is 1/5. Because the common ratio causes the numbers to get smaller and smaller, the sum is not infinite. Using the common ratio of 1/5 and the first term of a = 50, we can find the sum:
50 ÷ (1 - 1/5) = 50 ÷ 4/5 = 250/4 = 62.5
What this means is that if we keep adding numbers in the sequence, the sum will get closer and closer to 62.5.