Multiplying Two Matrices
Matrix Multiplication
Multiplying Two Matrices
To find the product of two matrices, such as matrix M and N, we need to look at the first row for matrix M and the first column for matrix N.
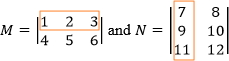
Once you find them, multiply corresponding elements, and find the sum of their products. You could interpret this as finding the dot product of the row and column.
(1 × 7) + (2 × 9) + (3 × 11) = 59
This is element a11 of the resultant matrix.
Now locate the first row for matrix M and the second column for matrix N. How can you find the second element for the resultant matrix?
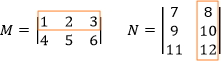
Once you find them, multiply corresponding elements, and find the sum of their products.
(1 × 8) + (2 × 10) + (3 × 12) = 64
This is element a12 of the resultant matrix.
For the next step we are going to repeat the same procedure, but this time we will work with the second row of M and the first column of N, followed by locating the second row of M and second column of N, and we obtain
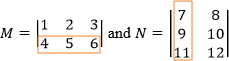
(4 × 7) + (5 × 9) + (6 × 11) = 132
This is element a21 of the resultant matrix.
and
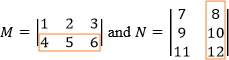
(4 × 8) + (5 × 10) + (6 × 12) = 154
This is element a22 of the resultant matrix.
Therefore, the resultant matrix is
Can These Matrices Be Multiplied Together?
If M is an x × y matrix, and N is a y × z matrix, then the product MN is an x × z matrix. Not all matrices can be multiplied together; to determine whether matrix M and N can be multiplied we need to look at the size of each matrix. The number of columns in M and the number of rows in N must be the same. Then you can multiply the matrices, and the values of x and z will determine the size of the resultant.
M * N = MN
x × y * y × z = x × z
So, if matrix A is 3 × 4 and matrix B is a 4 × 2, then AB is possible since 4 = 4, and the size of the resultant matrix is 3 × 2.
BA is not possible in this case because the number of columns in B is not the same as the number of rows in A (2 ≠ 3).
not possible
It is important to know that matrix multiplication is not commutative. Even if it's possible to multiply matrices M and N in both directions, MN ≠ NM.
Practice
Multiply if possible.
1)
2)
3)
4)
Answers
1)
2)
3) Not possible
4)
1)
2)
3) Not possible
4)