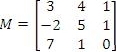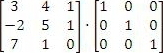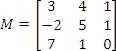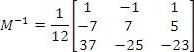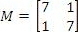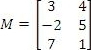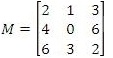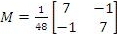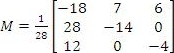Inverse Matrix
Identity Matrix
In algebra, we have the identity property for a real number m, where
m × 1 = m and 1 × m = m
for any real number.
For a square matrix M, the identity property is found by using a square identity matrix I, such that
M × I = M and I × M = M
where I and M must be square matrices of the same size.
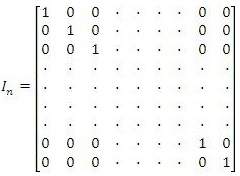
An identity matrix is a square matrix that features 1's along the top-left to lower-right diagonal, and zeroes everywhere else.
The 2 × 2 identity matrix is I2 = , and the 3 × 3 identity matrix is I3 = .
The n × n identity matrix is
Example
Verify the identity relation M × I = M using the following matrix M:
Setting this up,
Multiplying, we can find each of the elements of the product:
(3 × 1) + (4 × 0) + (1 × 0) = 3
(3 × 0) + (4 × 1) + (1 × 0) = 4
(3 × 0) + (4 × 0) + (1 × 0) = 1
(-2 × 1) + (5 × 0) + (1 × 0) = -2
(-2 × 0) + (5 × 1) + (1 × 0) = 5
(-2 × 0) + (5 × 0) + (1 × 1) = 1
(7 × 1) + (1 × 0) + (0 × 0) = 7
(7 × 0) + (1 × 1) + (0 × 0) = 1
(7 × 0) + (1 × 0) + (0 × 1) = 0
The resultant matrix is
Since this matrix is identical to M, the property holds.
(As an exercise, you can verify for yourself that I × M = M for the same matrix.)
Multiplicative InversesIf M is an n × n matrix, its inverse M -1 also has order n × n, and has to satisfy the following property:
MM -1 = In and M -1M = In
There are two things to remember about this:
1.) Only a square matrix can have an inverse.
2.) Even though m -1 = for any nonzero number m, this is not the case for matrices. M -1 ≠ .
The inverse matrix is useful because its property can "undo" matrix multiplication. (There is no matrix division.)
A × B = AB
A-1 × (AB) = (A-1A) × B = I × B = B
Notice that matrix multiplication has the associative property. However, it does not have the commutative property, so the original and inverse matrices have to be on the same side of the multiplication for the inverse property to work.
Cryptographers use matrices to encode a particular sequence of numbers before delivering it, and recipients of the message can use the inverse matrix to decode it.
Example
To send messages in secret, a cryptographer may use a coding matrix. An example of such a matrix M is shown below.
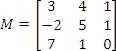
When a coded gets received by someone who knows the secret, he or she must use the inverse matrix to figure out the message. The inverse can be computed manually, but it's typically a long, tedious process, so the action may be best left to technology.
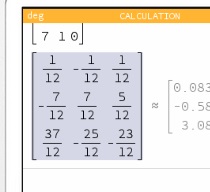
On most graphing calculators, you can use the brackets to create and invert a matrix: Use an open bracket to begin the matrix, then type out the elements one by one. Consult your calculator's manual for details on how you create the entries. Once the matrix is complete, raise it to the power of "−1" to compute the inverse.
(For those who wish to know how to find a matrix inverse manually, click here for a video that explains the process.) After inputting the commands, and converting the resulting numbers into fractions, we get this:
Since the numbers are fractions, we can factor out a common denominator to make the inverse easier to look at:
This is the inverse of the coding matrix. Let's see an example of how these matrices get used.
Suppose the following matrix contains an important message that needs to be delivered (an input sequence for a secret computer program, perhaps):
Multiply the matrices (M on the left) to put the message in code:
The matrix on the right is what gets sent out.
The recipient then left-multiplies the inverse matrix by the encrypted matrix to reveal the original message.
On a side note, you can verify that the matrix you get is the inverse by multiplying it by the original. No matter which way you multiply, the product should be the identity matrix.
M−1M =
MM−1 =
It checks out.
Exercises
If possible, find the inverse matrix for each of the following:
1)
2)
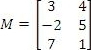
3) 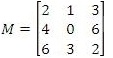
4)
Answers
1) 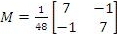
2) Not possible since M is not a square matrix
3) 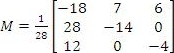
4)