Solving Systems of Equations
Solving Systems of Equations
There are three ways to solve a system of linear equations: graphing, substitution, and elimination.
Graphing Method
The solution to a system of linear equations is the ordered pair (or pairs) that satisfies all equations in the system. The solution is the ordered pair(s) common to all lines in the system when the lines are graphed.
Lines that cross at a point (or points) are defined as a consistent system of equations. The place(s) where they cross are the solution(s) to the system.
Parallel lines do not cross. They have the same slope and different y-intercepts. They are an example of an inconsistent system of equations. An inconsistent system of equations has no solution.
Two equations that actually are the same line have an infinite number of solutions. This is an example of a dependent system of equations.
Example
Solve the system of equations graphically.
3x + 2y = 4
−x + 3y = −5
Solution
Graph each line and determine where they cross.
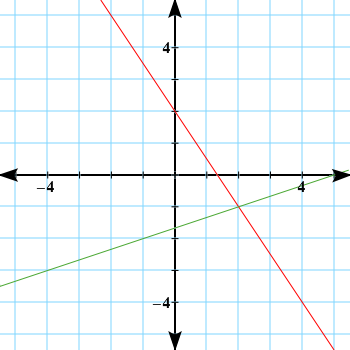
The lines intersect once at (2, −1).
A graphic solution to a system of equations is only as accurate as the scale of the paper or precision of the lines. At times the point of intersection will need to be estimated on the graph. When an exact solution is necessary, the system should be solved algebraically, either by substitution or by elimination.
Substitution Method
To solve a system of equations by substitution, solve one of the equations for a variable, for example x. Then replace that variable in the other equation with the terms you deemed equal and solve for the other variable, y. The solution to the system of equations is always an ordered pair.
Example
Solve the following system of equations by substitution.
x + 3y = 18
2x + y = 11
Solution
Solve for a variable in either equation. (If possible, choose a variable that does not have a coefficient to avoid working with fractions.)
In this case, it's easiest to rewrite the first equation by solving for x.
x + 3y = 18
x = −3y + 18
Next, substitute (−3y + 18) in for x into the other equation. Solve for y.
2( 3y + 12x + y = 11
2(−3y + 18) + y = 11-------Substitute -3y + 18 in for
−6y + 36 + y = 11-------Distribute.
2(
3y −5y + 36 = 11-------Combine like terms.
2(
3y + 18−5y = −25-----Subtract 36 from both sides
2(
3y + 18) + y = 5---- -Divide both sides by -5.
Then, substitute y = 5 into your rewritten equation to find x.
x = −3y + 18
x = −3(5) + 18
x = −15 + 18
x = 3
Identify the solution. A check using x = 3 and y = 5 in both equations will show that the solution is the ordered pair (3, 5).
Elimination Method
Another way to solve a system of equations is by using the elimination method. The aim of using the elimination method is to have one variable cancel out. The resulting sum will contain a single variable that can then be identified. Once one variable is found, it can be substituted into either of the original equations to find the other variable.
Example
Find the solution to the system of equations by using the elimination method.
x − 2y = 9
3x + 2y = 11
Solution
Add the equations.
x − 2y = 9
3x + 2y = 11
4x + 2y = 20
Isolate the variable in the new equation
4x = 20
x = 5
Substitute x = 5 into either of the original equations to find y.
x − 2y = 9
(5) − 2y = 9
−2y = 4
y = −2
Identify the ordered pair that is the solution. A check in both equations will show that (5, −2) is a solution.
It may be necessary to multiply one or both of the equations in the system by a constant in order to obtain a variable that can be eliminated by addition. For example, consider the system of equations below:
3x + 2y = 6
x − 5y = 8
Both sides of the second equation above could be multiplied by −3. Multiplying the equation by the same number on both sides does not change the value of the equation. It will result in an equation whereby the x values can be eliminated through addition.
Special Cases
In some circumstances, both variables will drop out when adding the equations. If the resulting expression is not true, then the system is inconsistent and has no solution.
4x + 6y = 13
6x + 9y = 173(4x + 6y = 13)
2(6x + 9y = 17)12x + 18y = 39
12x + 18y = 34
0 = 5
The equation is false. The system has no solution.
If both variables drop out and the resulting expression is true, then the system is dependent and has infinite solutions.
6x + 15y = 24
4x + 10y = 162(6x + 15y = 24)
3(4x + 10y = 16)12x + 30y = 48
12x + 30y = 48
0 = 0
The equation is true. The system has an infinite number of solutions. (Notice that both of the original equations reduce to 2x + 5y = 8. All solutions to the system lie on this line.)
Practice
Solve the following linear systems.
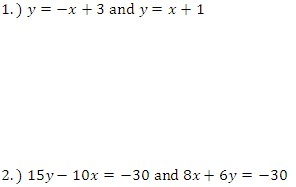
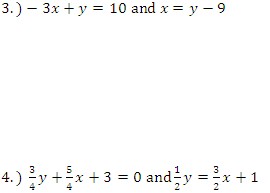
Answers