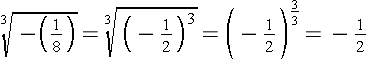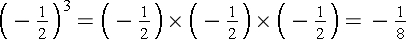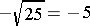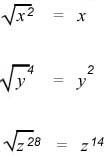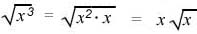Working with Roots and Radicals
The root of an expression is the reverse of raising it to a power:
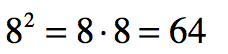
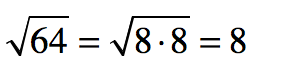
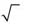 ) sign.
) sign. 
Radicals
The most common roots to work with are square roots. If no index number is present, the symbol stands for a square root.
However, not every radical is a square root. If there is an index number present other than the number 2, then the root is not a square root.
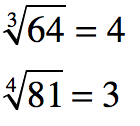
How Do You Know if the Root is Positive or Negative?
- A positive number times itself will yield a positive number.
- A negative number times itself will yield a positive number.
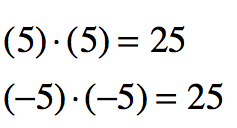
To show the negative of a square root, a negative sign would have to be placed outside the radical.
Example
To show the negative square root of 25, the negative sign goes outside the radical:
is not a real number
When working with other roots, note that when the index is odd, a negative radicand can be produced by negative factors.

To simplify square roots, we can make use of the product rule for square roots, which states that the product of two square roots is equal to the square root of the product for all real numbers.
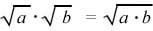
To Simplify the Square Root of a Constant:
1) Write the constant as a product of the largest perfect square factor and another factor.
2) Use the product rule to write the expression as a product of square roots, with each square root containing one of the factors.
3) Find the square root of the perfect square factor.
To Simplify Square Roots Containing Variables:
1) If the expression consists of a variable raised to an even power, the square root of the expression equals the variable raised to one-half of that power.
Examples:
2) If the variable contains an odd power, express it as the product of two factors, one having an exponent 1 and the other a perfect square.
3) Use the product rule to simplify.
Example:
Example
Simplify:
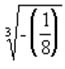

Result: