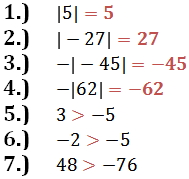Lesson - Absolute Value and Signed Integers
Absolute Value and Signed Integers
The absolute value of a number is the distance between the number and zero on a number line. The absolute value of a number n is written as |n|. The absolute value of 0 is 0.
Two numbers are opposites if they have the same absolute value but different signs. Opposites are the same distance from 0 on a number line, and they are on opposite sides of 0. The opposite of 0 is 0.
Examples
- The opposite of 5 is -5.
- The opposite of -12 is 12.
- Because |-9| = 9, the opposite of |-9| is -9.
Integers
Numbers greater than zero are called positive numbers. Numbers less than zero are called negative numbers. The collection of all numbers without fractional parts, both negative, positive, and zero are referred to as integers.

The integers are ... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...
Each integer can be shown on a number line. Placing a dot at the location of the number is called graphing the integer on the number line.
A number line can also be used to visualize the order relation between two integers. A number that appears to the left of a given number is less than (<) the given number. A number that appears to the right of a given number is greater than (>) the given number.
Example
Graph -3 and 1. Define their order relationship.
-3 < 1
Practice
Evaluate each.
1.) |5|
2.) |-27|
3.) - |-45|
4.) - |62|
Place the correct symbol, < or >, between the two numbers.
1.) 3 - 5
2.) - 2 - 5
3.) 48 - 76
Answer Key