The Pythagorean Theorem and its Converse
 Learning Target: I can use the Pythagorean Theorem to solve problems and determine whether given side lengths form a right triangle.
Learning Target: I can use the Pythagorean Theorem to solve problems and determine whether given side lengths form a right triangle.
Using the Pythagorean Theorem
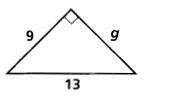
Find the value of g. Write your answer in simplest radical form.

Using the Pythagorean Theorem, substitute g and 9 for the legs and 13 for the hypotenuse.
a2 + b2 = c2
g2 + 92 = 132 Substitute
g2 + 81 = 169 Simplify
g2 = 88 Subtract 81 from each side
g2 = Take the square root
g = Simplify
You can simplify radicals by looking for square number factors.
You can also use the Pythagorean Theorem in the other direction (that is, use the converse of the Pythagorean Theorem) to determine whether a triangle is right.
Example 2
Is a triangle with sides of lengths 8, 12, and 14 a right triangle?
If this is a right triangle, then the sides should follow the Pythagorean Theorem, with the longest side being the hypotenuse.
a2 + b2 = c2
82 + 122 ? 142
64 + 144 ? 196
208 > 196
The theorem doesn't hold. So the triangle is not a right triangle.
As a bonus, however, we can figure out what kind of triangle this is.
If a2 + b2 > c2, the triangle is acute.
If a2 + b2 < c2, the triangle is obtuse.
Because 208 > 196, the triangle is acute.
Let's Practice Together
Find the missing side lengths. Leave your answers in simplest radical form.
1.
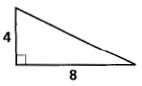
2.
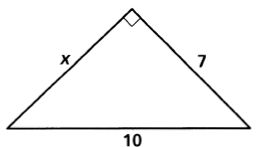
3. A triangle has side lengths of 12, 15, and 20. Is this triangle acute, right or obtuse?
Your Turn
Find the missing side lengths. Leave your answers in simplest radical form.
4.
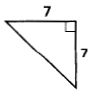
5.
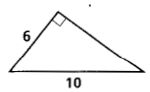
6.
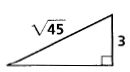
Find the value of each variable. Leave your answers in simplest radical form.
7.
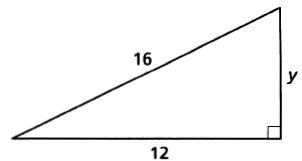
8.
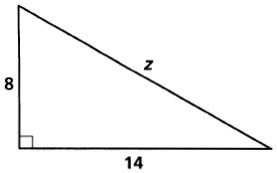
9.
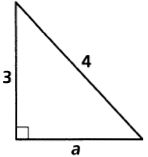
10.
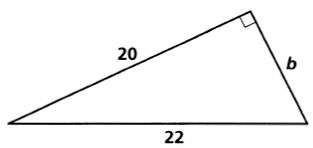
11.
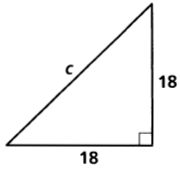
The numbers represent the lengths of the sides of a triangle. Classify each triangle as acute, obtuse, or right.
12. 6, 9, 10
13. 7, 24, 25
14. 18, 24, 30
15. 2, 5, 6
16. 20, 100, 110
17. 13, 21, 24
Check for Understanding
Find the area of each triangle. Leave your answers in simplest radical form.
1.
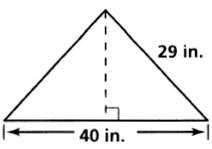
2.
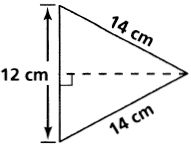
3.
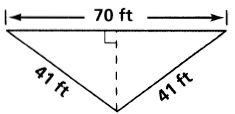
Answers
1.
2.
3. obtuse
4.
5. 8
6. 6
7.
8.
9.
10.
11.
12. acute
13. right
14. right
15. obtuse
16. obtuse
17. acute
Check for Understanding
1. 420 in2
2. cm2