Work Rate Problems
Work Rate Problems
For motion problems, we applied a formula concerning distance, rate, and time:
d = rt
In problems involving the rate of work, we will use a similar approach:
Strategy
For a job that can be completed in a certain amount of time t, the rate of work done per unit of time is . As a result,

So if we have r as the rate of work, t as the time taken to complete the job, and P as the amount of work completed, we have
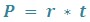
The amount of work completed is often measured in terms of the number of jobs carried out. For example, if one job is carried out in t seconds, then P = 1 and r = .
Example
One child can complete her homework twice as fast as her partner. When working together, both children can complete the homework in 45 minutes. If they work by themselves, how long will it take each child to complete the homework?
Step 1 — After reading the problem, we need to assign a variable. The variable will represent the amount of time that it takes the faster worker to complete the homework:
Let x = the time needed for the faster worker to complete the homework.
= rate of the faster worker
= rate of the slower worker
When both children work on the same assignment together, they take a total of 45 minutes.
Using this information, how can you figure out how much of the assignment each child did?
Strategy
Multiply each worker's rate by their shared time (45 minutes = ¾ of an hour). That product will show the fractional part of the homework that each child completed.
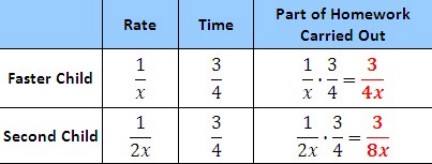
Step 2 – The sum of the two parts of the homework carried out is 1, since that one homework assignment was completed,
Now solve for x
The Alternate Route: You can do step 2 in a different way. Since the sum of the individual rates of each student equals their rate when working together, you can also use that information to solve for x.
Since x = = 67.5 minutes, we can say that the faster child will take 67.5 minutes to complete homework by herself, while the second child will take 135 minutes (67.5 × 2).
Does this answer make sense? These times seem reasonable since the time that it takes both children working together, 45 minutes, is less than the amount of time it takes the faster child to complete the assignment by herself, 67.5 minutes.
Practice
1. A couple works together to assemble a table in 1.5 hours. If the experienced worker can complete the job in 1/3 the time of the inexperienced worker, how long would it take each person to complete the job individually?
2. Carlos can clean up a pool in 5 hours, while Brianna can do it in 3/4 of the time it takes Carlos. How long will it take to clean the pool if both people are working together?
Answers
1) Experienced: 2 hours, inexperienced: 6 hours
2) 2 hours
3) 1 hours