Graphing Linear Inequalities
Graphing Linear Inequalities
Examples of linear inequalities in two variables:
y ≤ 2x + 5
2x + 5y < 7
4x + y ≥ -6
To graph a linear inequality in two variables, first graph the line as if it were a linear equation. Identify whether the inequality includes the "or equal to" aspect. Represent inequalities that do not include the possibility of "or equal to" with a dashed line and then shade the region that includes solutions to the inequality.
Steps to Graphing Inequalities:
Step 1 Change the inequality symbol to "=". Graph the equation. Use a dashed line for < or >. Use a solid line for ≤ or ≥.
Step 2 Test a point that is not on the line to check whether it is a solution of the inequality.
Step 3 If the test point is a solution, shade its region. If the test point is not a solution, shade the other region.
Example
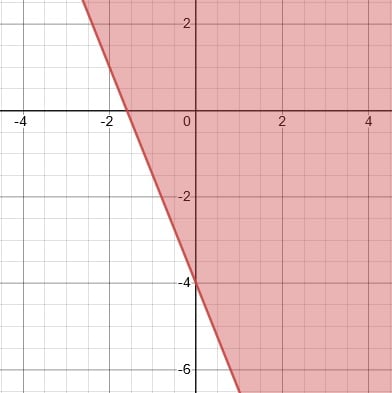
Graph: y − 2x > 3
First change > to = and write the equation in slope-intercept form:
y − 2x = 3
y = 2x + 3
The slope is 2 and the y-intercept is 3. Graph the line that passes through point (0, 3) and has a slope of 2. The line needs to be dashed because this is an inequality.
Using (0, 0) as a test point we need to find out which side provides a solution:
y > 2x + 3
0 > 2(0) + 3
0 ≯ 3
The inequality doesn't hold, so (0, 0) is not a solution. We then shade the half-plane that does not contain (0, 0).
You can apply the information from a graph of an inequality to extrapolate data (that is, get information for data points that aren't explicitly mentioned) or to answer questions.
Example
You are buying art supplies for your art club. You have $40 to spend. Tubes of paint cost $6 each, and brushes cost $4 each. This situation can be expressed with the inequality 6x + 4y ≤ 40, where x represents the number of tubes of paint, and y represents the number of brushes.
How many tubes of paint and how many brushes can you buy with $40?
Solution
Graph the inequality where the equation of the line is 6x + 4y = 40. It may help to convert the equation into slope-intercept form: y = −x + 10. Then test it at point (0, 0), which gives:
6(0) + 4(0) ≤ 40
0 ≤ 40
The inequality holds, so (0, 0) is a solution. Shade the half-plane that contains (0, 0).
b. Use the graph to find a solution, then interpret the solution.
One solution is (4, 4).
This means that you can buy 4 tubes of paint and 4 brushes.
Practice
Graph the following inequalities.
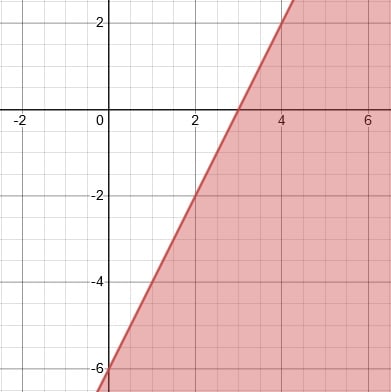
1. y ≤ 2x − 6
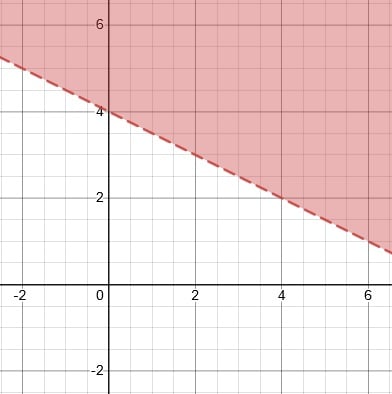
2. y > −x + 4
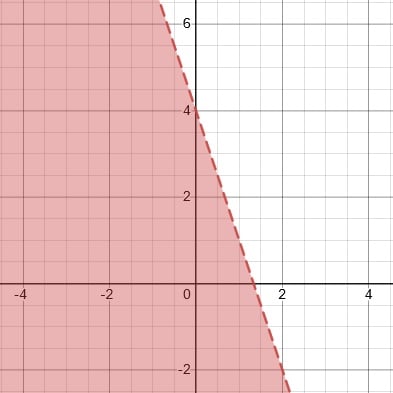
3. 3x + y < 4
4. 5x + 2y ≥ −8
Answers
1.
2. 
3.
4.