Roots of Polynomial Functions
Theorems about Roots
of Polynomial Equations
You can write a polynomial equation by using its roots.
Example
Find a third-degree polynomial equation with rational coefficients that has roots −4 and 2 − 3i
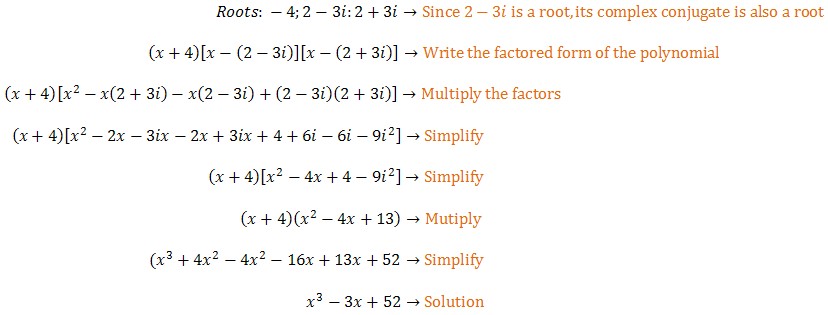
A third-degree polynomial equation with rational coefficients and roots −4 and 2 − 3i is
x3 − 3x + 52 = 0
Fundamental Theorem of Algebra
When working with polynomial equations and finding their roots, you might have noticed something: The number of roots always seems to match the degree of the polynomial. That's no coincidence.
The Fundamental Theorem of Algebra states that the degree of a polynomial is the maximum number of roots the polynomial has. A third-degree equation has, at most, three roots. A fourth-degree polynomial has, at most, four roots.
If you count repeated roots as many times as they appear, then the degree of the polynomial will be the exact number of roots. Think about quadratic equations:
x2 + 5x + 6 = 0
(x + 2)(x + 3) = 0
x = {−2, −3}
x2 − 2x + 5 = 0
x =
x = {1 + 2i, 1 − 2i}
x2 − 6x + 9 = 0
(x − 3)(x − 3) = 0
x = 3 (mult. 2)
Counting the repeated root in the third equation twice, all these equations have two roots, and the degree of each equation is 2.
Practice
Find a third-degree polynomial equation with rational coefficients that has the given roots. Let the leading coefficient be 1.
1.) 1; 2 − i
2.) 5 + 2i; −2
3.) 3i; 7
4.) 2 + 5i; 3
A polynomial equation with rational coefficients has the given roots. Find two additional roots.
5.) −4i; 6 − i
Find a fourth degree polynomial equation with integer coefficients that has the given numbers as roots. Let the leading coefficient be 1.
6.) 2i; 4 − i
Answer Key
1.) x3 − 5x2 + 9x − 5 = 0
2.) x3 − 8x2 + 9x + 58 = 0
3.) x3 − 7x2 + 9x − 63 = 0
4.) x3 − 7x2 + 41x − 87 = 0
5.) 4i, 6 + i
6.) x4 − 8x3 + 21x2 − 32x + 68 = 0