Quadratic & Polynomial Equations
Quadratic Formula
It is often considered easiest to solve quadratic equations by factoring. However, for quadratics that are not factorable, the quadratic formula can be applied to find solutions. The quadratic formula is derived from the process of completing the square, and it works on every equation.
To solve quadratic equations:
1. Try to factor.
2. If factoring is not possible, use the quadratic formula --
where ax2 + bx + c = 0
Note: i =
, so
.
Using the Discriminant
The value under the radical sign, b2 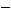 4ac, is called the discriminant. The value of the discriminant tells you a lot about the solutions of the equation:
4ac, is called the discriminant. The value of the discriminant tells you a lot about the solutions of the equation:
- If the value of the discriminant is positive, there are two real solutions for x, meaning the graph of the solution has two distinct x-intercepts.
- If the value of the discriminant is zero, there is one real solution for x, meaning the graph of the solution has one x-intercept.
- If a negative number is inside the square root, there are no x-intercepts. The solutions are not real numbers, but would have to be expressed as complex numbers.
| a positive number inside the square root | zero inside the square root | a negative number inside the square root |
| two real solutions | one (repeated) real solution | two complex solutions |
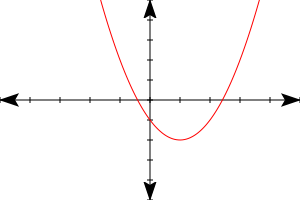 | 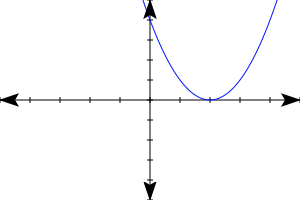 |  |
| two distinct x-intercepts | one (repeated) x-intercept | no x-intercepts |