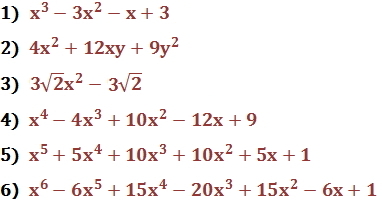Expand Polynomials

---

A polynomial is expanded if no variable appears within parentheses and all like terms have been combined.

To expand a polynomial, multiply its factors (often by using the distributive property) or perform the indicated operations.  Then combine all like terms. 

Example

Expand the following expression.

3x(4 − x) + (2x − 5)²

Remembering the order of operations, we take care of exponents before multiplication.

Because (2x − 5)² = (2x − 5)(2x − 5), recall that we can use the FOIL method to multiply this out, then combine like terms:

(2x − 5)(2x − 5) = 4x² − 10x − 10x + 25

= 4x² − 20x + 25

Now we have:

3x(4 − x) + (4x² − 20x + 25)

Multiply the 3x by (4 − x) using the distributive property:

(12x − 3x²) + (4x² − 20x + 25)

Now all that's left is to add the polynomials by combining like terms.  Remember, when complete, the polynomial is written in standard form, so the exponents are in descending order:

(12x − 3x²) + (4x² − 20x + 25) = -8x + x² + 25 = x² − 8x + 25

---

Practice

1)    (x + 1)(x − 1)(x − 3)

 

 

 

 

2)    (2x + 3y)² 

 

 

 

 

3)    (x + )(x − )

 

 

 

 

4)    (x²  − 2x + 3)²

 

 

 

 

5)    (x + 1)⁵

 

 

 

 

6)    (x − 1)⁶

---

---

Answer Key