Permutations and Factorials
Permutations and Factorials
In some arrangements of groups, order is important. For example, the diagram shows the different ways that a group of three dogs could finish first, second, and third at a dog show.

Each arrangement lists the same dogs, but the orders are different. Arrangements such as these are called permutations. A permutation is an arrangement in which order is important. You can use the counting principle to count permutations.
Counting Permutations
You have five CDs. You can use the counting principle to count the number of permutations of 5 CDs. This is the number of different orders in which you can listen to the CDs.

You can listen to the CDs in 120 different orders.

Practice
Evaluate each factorial.
1. 4!
2. 1!
Example
Counting Permutations
Twelve marching bands are entered in a competition.
You can use the counting principle to count how many ways first, second, and third places can be awarded.
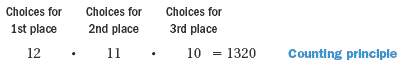
There are 1320 ways to award the three places.
Permutation Notation
The above example shows how to find the number of permutations of 12 objects takes 3 at a time. This is written 12P3. Therefore, 12P3 = 1320.
In general, the number of permutations of n objects taken r at a time can be written as nPr and evaluated using 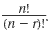
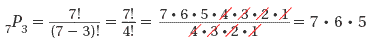
Example 2
Two students are chosen from a group of 6 to read the first and second poems at the school's poetry reading.
To find how many different ways the students can be chosen, find 6P2.
Step 1 Use the formula.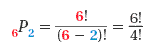
Step 2 Divide out common factors.
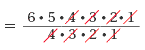
Step 3 Multiply.
6 x 5 = 30
There are 30 ways the speakers can be chosen.
Practice
3. Find the number of permutations.
100P2
4. Find the number of permutations.
8P6
5. Find the number of permutations.
7P7
6. Complete the sentence.
The number of permutations of 15 objects taken 7 at a time can be written as _?_.
7. Evaluate.
0!
8. You have three things to do after you wake up tomorrow. You need to take a shower, eat breakfast, and call your friend. Find the number of permutations and list them.
9. You go to the cafeteria with five friends. In how many different orders can you and your friends get into the lunch line?
10. Your softball team has 15 players. Find the number of different ways that the first, second, third, fourth, and fifth batters can be chosen.
Answers
1. 24
2. 1
3. 9,900
4. 20,160
5. 5,040
6. 15P7
7. 1
8. shower-breakfast-friend, shower-friend-breakfast, breakfast-shower-friend, breakfast-friend-shower, friend-shower-breakfast, friend-breakfast-shower
9. 720
10. 360,360