Combinations
Combination
In permutations the order in which something is arranged is important.
A combination on the other hand is a group of items whose order is not important. For example, suppose you go to lunch with a friend. You choose milk, soup, and a salad. Your friend chooses soup, a salad, and milk. The order in which the items are chosen does not matter. You both have same meal.
Listing Combinations
Example
You have 4 tickets to the county fair and can take 3 of your friends. You can choose from Abby (A), Brian (B), Chloe (C), and David (D). How many different choices of groups of friends do you have?
Solution
List all possible arrangements of three friends. Then cross out any duplicate groupings that represent the same group of friends.

You have 4 different choices of groups to take to the fair.
Practice
1. In the example above, the complete list shows the number of permutations of 4 items chosen 3 at a time. How many items would be in the complete list if you had to choose from 8 friends?
Combination Notation
In Example 1, after you cross out the duplicate groupings, you are left with the number of combinations of 4 items chosen 3 at a time. Using notation, this is written 4C3.
Combination Notation
To find the number of combinations of n objects taken r at a time, divide the number of permutations of n objects taken r at a time by r!.
Formula: Example: 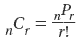
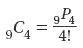
Evaluating Combinations
Find the number of combinations.
Example
8C3
Example
9C7
Practice
Find the number of combinations.
2. 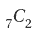
3. 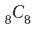
4. 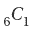
Permutations and Combinations
State whether the possibilities can be counted using a permutation or combination. Then write an expression for the number of possibilities.
a. There are 8 swimmers in the 400 meter freestyle race. In how many ways can the swimmers finish first, second, and third?
Solution: Because the swimmers can finish first, second, or third, order is important. So the possibilities can be counted by evaluating 8P3.
b. Your track team has 6 runners available for the 4-person relay event. How many different 4-person teams can be chosen?
Solution: Order is not important in choosing the team members, so the possibilities can be counted by evaluating 6C4.
Practice
5. Complete the statement: The expression 9C5 represents the number of combinations of _?_ objects taken _?_ at a time.
6. You choose 3 art projects from the following list: clay, plaster, wood, wire, drawing, painting. Describe and correct the error below in finding the number of possible combinations of 3 projects.
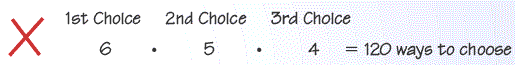
Tell whether the possibilities should be counted using a permutation or combination. Then find the answer.
7. You are buying balloons for a party. The store has four different colors, and you would like to choose two different colors. How many different pairs of balloon colors can be chosen?
8. You must do homework in math, history, science, and geography. In how many different orders can you do your homework?
9. Your hockey team is choosing 2 team captains from its 18 members. Find the number of different ways this can be done.
10. A debate team has 5 members. Your debating club has 12 students. How many different teams can be chosen?
11. You are at a fair with four friends. All of you want to ride the roller coaster, but only three people can fit in the first car. How many different orderings of three can you and your friends make?
12. You have 6 different sweatshirts, and you want to donate some to a charity. Draw a diagram or write an expression so that you can find the number of ways you can donate 2 sweatshirts. Then find the number of ways you can donate 3 sweatshirts.
13. You are shopping for a trip and want to buy three sweaters from among a red sweater, a blue sweater, a plaid sweater, a striped sweater, and a turtleneck sweater. How many sets of three sweaters can you choose?
14. You want to know the number of ways you can play your six favorite songs.
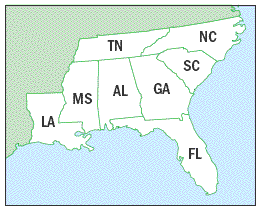
15. You are coloring the map shown below. You want each state to be a different color, and you have 10 possible colors. In how many ways can you color the map? In how many ways can you choose 8 colors?
Answer Key
1. 336
2. 21
3. 1
4. 6
5. 9, 5
6. You also need to divide by the number of orderings of the smaller group. The correct number of combinations is 20.
7. combination: 6
8. permutation: 24
9. combination: 153
10. combination: 792
11. permutation: 24
12. combination: 15; 20
13. combination: 10
14. permutation: 720
15. permutation: 1,814,400; combination: 45