1-to-1 Functions
1-to-1 Functions
A 1-to-1 function passes a vertical line test and a horizontal line test.
This record is not due to good test-taking skills, but it is due to the function's domain and range. Every x-value of a 1:1 function can yield only one possible value of y (as with any function), and every y-value corresponds with only one value of x.
Which of the following graphs shows a 1:1 function?
y2 = x
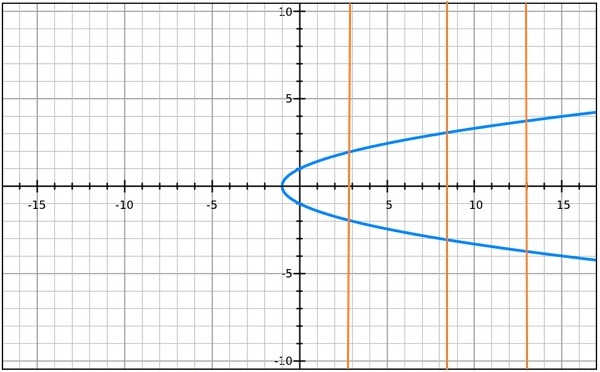
This equation does not pass the vertical line test, so it is not a function. On this graph, most values of x have more than one possible value of y.
y = x2 +1
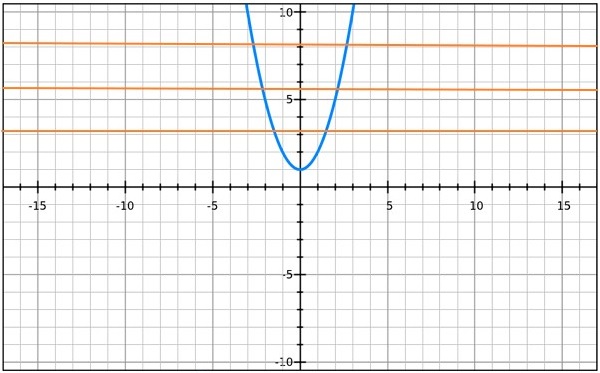
This equation is a function, but it does not pass the horizontal line test. On this graph, most values of y have more than one possible value of x.
y = 2x + 1
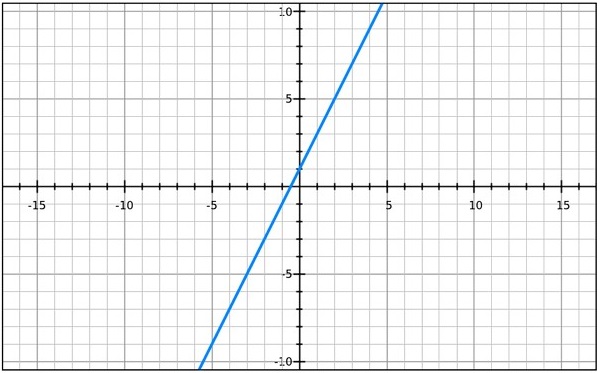
The line above represents a 1-to-1 function because each value of x can only yield a single value of y, and vice versa.
But what if you don't have a graphing calculator? How can you determine if a function is a 1-to-1 function?!
Mathematicians have come up with a test:
If f(p) = f(q), then p = q. If this fact holds, then congratulations! You have a 1-to-1 function.
If our function is f(x) = 2x + 1, then
f(p) = f(q)
2p + 1 = 2q + 1
2p + 1 − 1 = 2q + 1 − 1
2p = 2q
p = q
The fact holds, so the function is 1-to-1.
Let's try another example:
If our function is f(x) = 2x2 + 1, then
f(p) = f(q)
p2 + 1 = q2 + 1
p2 + 1 − 1 = q2 + 1 − 1
p2 = q2
±p = ±q
The answer to a square root can either be positive or negative, so p and q are not necessarily equal. Either p = q, or p = −q. Therefore, the fact does not hold, and the function is not 1-to-1.