Right Triangle Relationships
Right Triangle Relationships
Right triangles are often used when finding locations because a direct, slanted distance can be expressed in terms of easily measured horizontal and vertical distances.
The Pythagorean Theorem shows how the hypotenuse, c, of a right triangle is related to its legs, a and b.
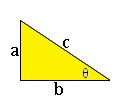
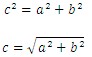
Given one of the sides and the hypotenuse, the other side can be found by solving for either a or b.
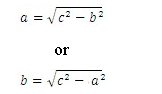
Example
A government agency decides to build a memorial park in the shape of a right triangle. They decide that the longest side will be 30 yards longer than 3 times the length of the shortest side. If the hypotenuse will be 15 yards longer than the longest side, what are the sides of the triangle?
Let x be the length of the shortest leg, so if we use the a, b, and c notation we have
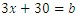
where b is the length of the longest leg.
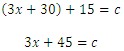
where c is the length of the hypotenuse. Let us write the equation now and then solve for x.
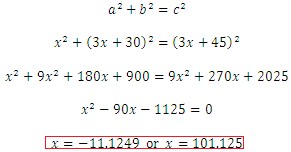
Does it make sense? Since the sides of the triangle represent a length, an answer of -11.1249 does not seem reasonable. So, using our second value we find that
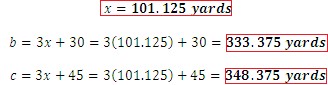
Ratios to Remember
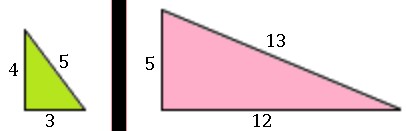
There are several examples of right triangles, but there are two common ratios for side a: side b: side c. One example is the 3-4-5 triangle:
length of side a : length of side b: length of side c = 3:4:5
Another one of these relationships is the 5-12-13 triangles. You can use the Pythagorean Theorem to test these relationships.
Special Triangles
Right triangles with angles that measure 45o- 45o- 90o or 30o- 60o- 90o are called special right triangles. They obey the theorems below.
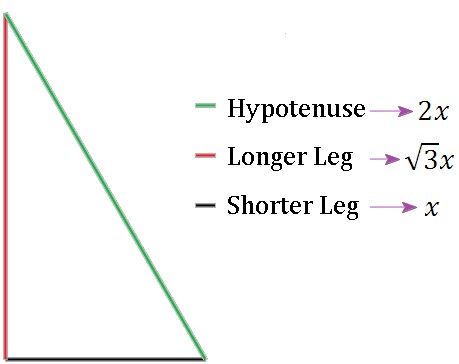
30o- 60o- 90o Triangle Theorem
In a triangle that has the angles 30, 60, and 90 degrees, the hypotenuse is 2 times as long as the shorter leg, and the longer leg is times as long as the shorter leg.
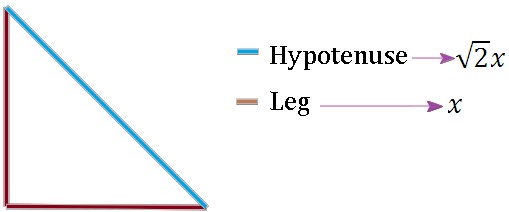
45o-45o-90o Triangle Theorem
In a triangle with the angles 45o, 45o, and 90o, the hypotenuse is times as long as each leg.
Example
Find the length of side L and hypotenuse H:
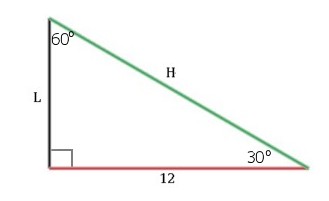
Because the triangle has 30-, 60-, and 90-degree angles,
we can use the 30o-60o-90o Triangle Theorem.


Example
Find the length of s in the following triangle:
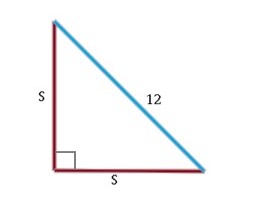
Because this shape is a right triangle, and the two sides have the same length, s, it must be a 45o- 45o- 90o triangle. So, we can use that theorem to solve for s.

Guided Practice
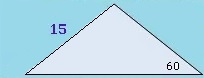
1. Stage Height
a. A rock band uses a ramp at a theater to load and unload the equipment from the main stage. If the ramp is 20 meters long and has an incline of 30 degrees, how high is the main stage?
b. How high is the main stage if the ramp has an incline of 60 degrees?
c. How high is the main stage if the ramp has an incline of 45 degrees?
2. Find the unknown lengths of the sides in the triangles below:
a. What is the length of the hypotenuse?
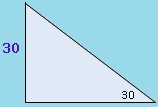
b. What is the height of this isosceles triangle?
c.What is the length of each leg?
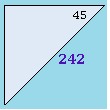
Answers
1. a. 10 m b. m c. m
2. a. 60 b. c.