The Metric System/ SI-Units
Metric System/International System of Units (SI)
The metric system is used by scientists, many military units, and all industrialized nations outside the U.S. As a result, this system is important to learn in order to develop your career and travel.
Length
millimeters < centimeters < meters < kilometers
These are the four metric units that are commonly used to measure length. There are many more units that are much shorter than millimeters and much longer than kilometers. Each unit is based on the meter. Its length is some multiple of 10 times the length of a meter.
For example: I kilometer = 1 meter x 103
Converting between two metric units just required multiplying by a power of 10.
Here are the most common conversions you'll make in class, on tests, and on trips:
- 1000 millimeters = 1 meter
- 100 centimeters = 1 meter
- 1000 meters = 1 kilometer
As NASA's website explains, all units under a meter use Latin roots. "Milli-" comes from the Latin for 1000, and "centi-" comes from the Latin for 100. These prefixes represent 1/1000 and 1/100 of a unit respectively.
Units that are greater than a meter use Greek roots. "Kilo-" comes from the Greek for 1000, and represents 1000 units. There is also a Greek prefix "hecto-" for 100 units, though it's not commonly used.
You can use the table below to practice conversion problems:
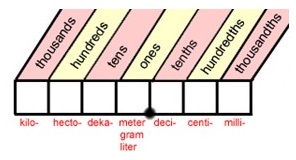
Convert 0.5 meters to centimeters.
1 meter = 100 centimeters
We can set up a proportion to solve:
Cross-multiply to solve for x.
x = 0.5 x 100
x = 50 centimeters
Convert 0.5 meters to kilometers.
1 kilometer = 1000 meters
We can set up a proportion to solve:
Cross-multiply to solve for x.
1000x = 0.5
x = 0.5/1000
x = 0.0005, or 5 x 10-4 kilometers
ADD MIXED UNITS
4 cm 11 mm + 5 cm 2 mm = ?
To set up this problem, make sure each value is lined up with values that have the same unit.

Start by adding the values in the right column.
11 mm + 2 mm = 13 mm
Because there are 10 mm in 1 cm, carry a centimeter from the millimeters column into the centimeters column. The 3 mm left over stays in the right column (the process is just like regular arithmetic).

Now add up the centimeters.

The sum is 10 cm 3 mm.
Weight/Mass
milligram < grams < kilograms
These prefixes will look familiar, and they have the same meanings:
- 1000 milligrams = 1 gram
- 1000 grams = 1 kilogram
Convert 200 grams to milligrams and kilograms.
To go from grams to milligrams, set up this proportion:
x = 200 x 1000
x = 200,000 milligrams
Use this proportion to go from grams to kilograms:
1000x = 200
x = 0.2 kilograms
Capacity/Liquid Volume
milliliters < liters
(These are the most commonly used units.)
Liquid Volume
- 1000 milliliters = 1 liter
0.75 liters of water is equal to how many milliliters?
We can set up a proportion to solve:
Cross-multiply to solve.
x = 1000 x 0.75
x = 750 milliliters
Liquid Volume to Solid Volume
You may also be asked to figure out how many milliliters of water will completely fill a solid container. In this case, you can convert the volume of a solid object to liquid volume. Here are the key conversion rates:
- 1 cubic millimeter = milliliter
- 1 cubic meter = 1000 liters
If Leigh needs to take 2 liters of water to a training session, what is the minimum volume of the container in which she can carry that water to her session?
We can set up another proportion by using the conversion rate for cubic meters and liters.
1000x = 2
x = 2/1000
x = 0.002 cubic meters
If you memorize the value each prefix represents, you'll be ready to take on measurements like the deciliter, and also understand some other frequently used terms like the kilobyte, megabyte, and gigabyte.