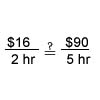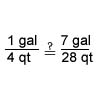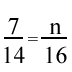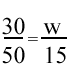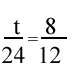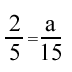Proportional Relationships
Learning Target: I can use cross-products to determine whether an equation represents a true proportion.
Proportions
- A proportion is an expression of the equality of two ratios or rates.
- A proportion is true if the fractions are equal when written in lowest terms.
Example 1
- Any units expressed in a proportion must be consistent. (When units are used, the units of the numerators are the same, and the units of the denominators are the same.)
- In any true proportion, the "cross products" are equal.
Solving Proportions
Sometimes one of the numbers in a proportion is unknown. In this case, it is necessary to solve the proportion.
To solve the proportion, find a number to replace the unknown so that the proportion is true. You can use cross-products to solve a proportion.
Example 2
Proportions are helpful when solving problems that require for a scale or rate to be followed.
When writing a proportion to solve a problem, be sure to use follow a consistency of units.
Example 3
A bakery makes two kinds of pies: cherry and apple. The ratio of cherry pies to apple pies is 5 to 9. If there are 70 pies in all, how many are cherry?
Step 1: Determine the ratio of cherry pies to total pies.
For every 14 pies, 5 are cherry.
Step 2: Set up a proportion of cherry pies to total pies to find the number of cherry pies at the bakery.
5 x 70 = 14 c Cross products property.
Divide each side by 14.
25 = c Simplify.
There are 25 cherry pies at the bakery.
Let's Practice Together
1.) Determine whether the proportion below is a true proportion.
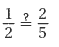
2.) Solve the proportion.
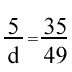
Your Turn
3.) Use cross products to determine whether each proportion given below is a true proportion.
a.)
b.)
3.)
4.) Solve each proportion. Round to the nearest hundredth if needed.
a.)
b.)
c.)
d.)
5.) Solve the following problems using a proportion.
a.) The dosage of a certain medication is 2 ounces for every 50 pounds of body weight. How many ounces of medication are required for a person who weighs 175 pounds?
b.) Three tablespoons of fertilizer are added to every 4 gallons of water. How many tablespoons of fertilizer are required for 10 gallons of water?
Check for Understanding
1.) The scale on a map is 1.25 inches equals 10 miles. How far apart in miles are two towns that are 2 inches apart on the map?
2.) A contractor charges $9.25 per square foot for stucco work. A homeowner was given the estimate of $5,550 for stucco work on her home. What was the square footage used for the estimate?
1.) not true
2.) d = 7
3.)
a.) not true
b.) not true
c.) true
4.)
a.) n = 8
b.) w = 9
c.) t = 16
d.) a = 6
5.)
a.) 7
b.) 7.5
Check for Understanding
1.) 16 miles
2.) 600