Weighted Average
Weighted Average
Many word problems ask students to calculate the average (arithmetic mean) of a set of test scores.
Most final grades, however, are based on more than one set of data. Here's an example:
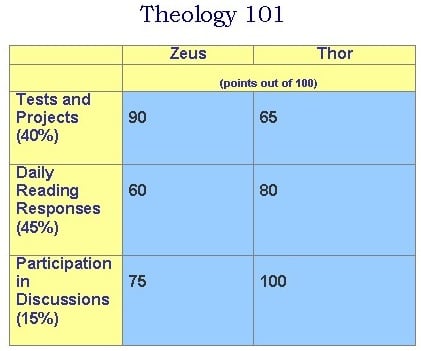
Which student will have the highest final average for Theology 101?
The way to figure this out is to multiply each score by its weight (percentage) and add the products together, then divide by the sum of the weights.
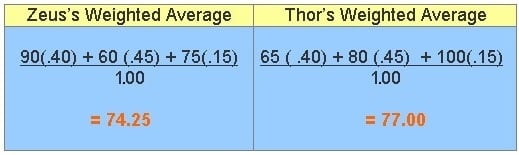
These scores are the student's weighted average. In a single set of test scores, each score, or quantity, is equally valuable. The quantities in a weighted average, however, are each given a particular weight, or value.
Average (Arithmetic Mean):
Weighted Average:
In the case of Theology 101, test and projects were given a higher value (that is, more weight) than participation.
You can use a weighted average to help you keep track of your grades and make important decisions based on what you value most.
Practice
Eddie needs to maintain an average of 85 or above in statistics in order to be accepted into the major.
His teacher's grading policy is below:
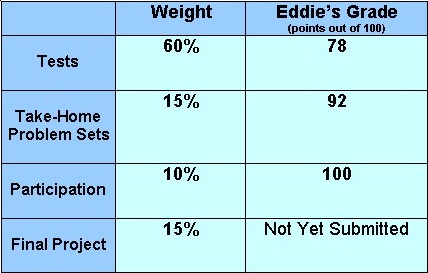
1. What is his average grade so far (without the final project)?
2. What grade does he need to earn on the final project in order to be accepted into the major?
Answers
1. about 83
2. 96
1. about 83
2. 96