Fractions
Fractions
A fraction can represent the number of equal parts of a whole.
Each part of a fraction has a name.

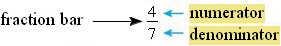
This fraction is read "four sevenths"
A proper fraction is less than 1. The numerator of a proper fraction is smaller than the denominator.

The expression above is
A mixed number is a number greater than 1 with a whole-number part and a fractional part.

The expression above is 1
An improper fraction is a fraction greater than or equal to 1. The numerator of an improper fraction is greater than or equal to the denominator.

The expression above is
Equivalent Fractions
Equal fractions with different denominators are called equivalent fractions.
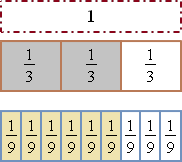
Remember that the Multiplication Property of One states that the product of a number and one is the same number. This is true for fractions as well as whole numbers. This property can be used to write equivalent fractions, where any fraction whose numerator and denominator are the same equals 1, then
where equals 1
Multiplying by a fraction equivalent to 1 can be used to find an equivalent fraction with a desired denominator.
Example
Find a fraction equivalent to 1/6 that has a denominator of 24
Simplify Fractions
A fraction is in simplest form when there are no common factors in the numerator and the denominator.
There is more than one way to reduce a fraction to its simplest form.
| You can cancel common factors | Divide the numerator and denominator by GCF of the numbers |
12 = 2  2 2 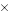 3 and 18 = 2 3 and 18 = 2 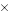 3 3 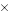 3 3Therefore the GCF of 12 and 18 is 2 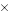 3 = 6 3 = 6 |
Try it yourself
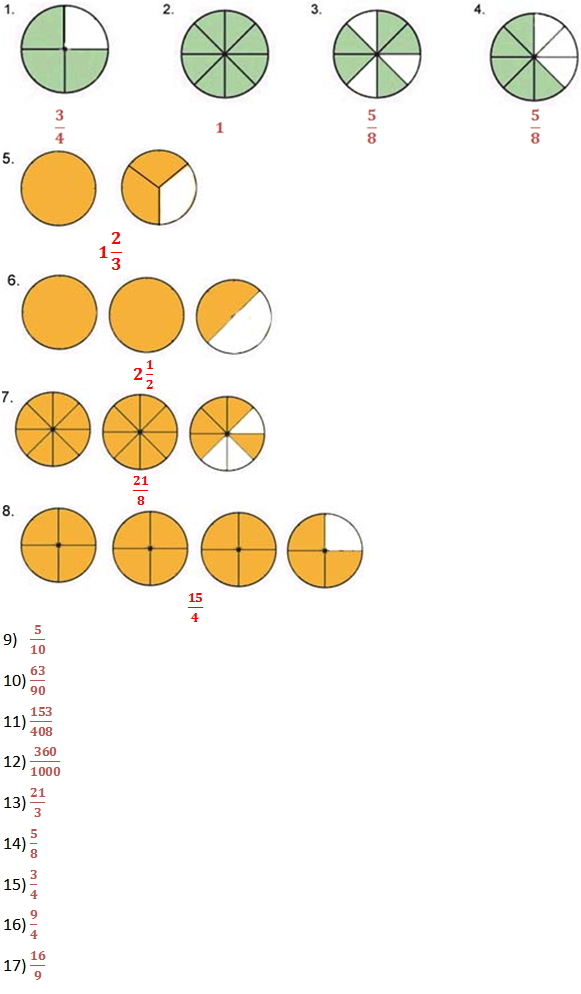
Express the shaded portion of the circle as a fraction.
1.)
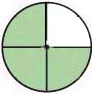
2.)
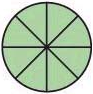
3.)
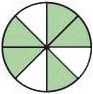
4.)
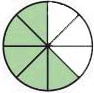
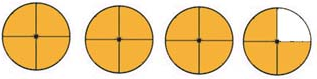
Express the shaded portion of the circles as a mixed number.
5.)
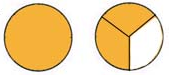
6.)

Express the shaded portion of the circles as an improper fraction.
7.)
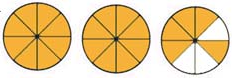
8.)
Write an equivalent fraction with the given denominator.
9.)
10.)
11.)
12.)
13.) 7
Write each fraction in simplest form.
14.)
15.)
16.)
17.)
Answer Key