Function Notation
Function Notation
When a function is expressed as an equation, it is often written as "f(x)." In creating a table of values for an equation, for example y = 5x − 1, we use this rule, "multiply by five and subtract one" to transform an input x value into the one resulting y value. By giving the expression "multiply by five and subtract one" the name f, we have an easy way to show that we're applying the rule to different numbers and variables.
In general, the symbol f(x) replaces y and is read as f of x, which does not mean f times x. It means the value of expression f for a given value of x.
Example
Evaluate the function for the given value of the variable.
f(x) = 5x − 1 when x = 3

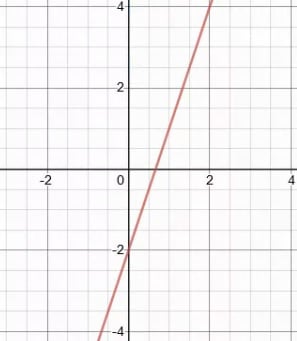
Graphing a Linear Function
Since the function notation lets us write f(x) instead of y, the graph of a function f is the set of all points (x, f(x)), where x is in the domain of the function.
Example
Graph f(x) = 5x − 1 and find the value of f(3) by using the graph.
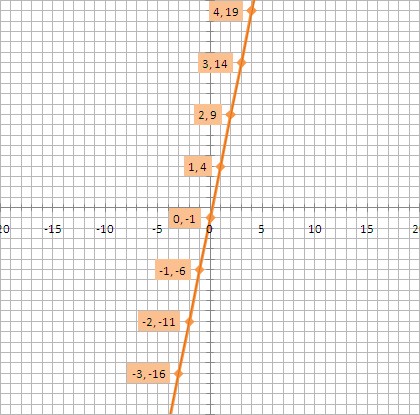
The y-intercept is -1 and the slope is 5. When x = 3, y equals 14. This confirms the answer found in the previous example.