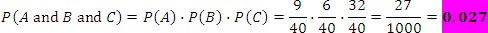Probability of Independent Events
Probability of Independent and Dependent Events
Probability of Independent Events
Two events are independent if the occurrence of one has no effect on the occurrence of the other. For example, when you toss a coin twice, the outcome of the first toss, either heads or tails, has no effect on the outcome of the second toss. Algebraically, if A and B are independent events, then the probability that both A and B occur is
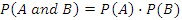
Example
You are playing darts with your friends and you have two more shots. What is the probability that you hit 4 or less with your first shot, and 18 with your second shot?
Let event A be getting a score less than 4 points, and let event B be hitting 18 on your second shot. The two events are independent, therefore the probability is
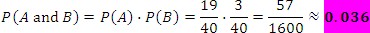
This result gives us the probability of the two independent events. This can be extended to the probability of three or more independent events.
Example
In the same game your friend has three shots. What is the probability of your friend scoring 4 on his first throw, 10 or higher on his second, and hitting anything but 6 on his third shot?
Let event A be the first shot where your friend hits a 4, let event B be the second shot where you friend hits 10 or higher, and let event C be the third shot where your friend hits anything but 6.