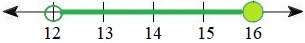Systems for Expressing Sets

A set is an assortment of distinctive components that do not repeat. Sets can be defined in different forms. Here are four common methods of interpreting them.

Set-Builder Notation

Set-builder notation is a mathematical coding system that shows the properties that the components of a set need to satisfy. A simple example is written as

{a | a ≤ 3}

which is expressed as the set ("{  }") of all a ("a"),such that (" | ") a is less than or equal to three ("a ≤ 3"), which can also be expressed as any value less than or equal to 3.

Example

Describe the following set:

x = {−1, 0, 1, 2, 3}

In set-builder notation, this set is written as:

{x ∈ ℤ | −1 ≤ x ≤ 3}

This set is described as all integer numbers that are less than or equal to three and equal to or greater than negative one, or all integer numbers between -1 and 3 inclusive.  The bold "Z" in the expression indicates that the x-values in the set are limited to the integers.

Roster Notation

A roster is a list of the elements in a set. They are surrounded by braces and separated by commas.

Example

Write in roster notation all the integer numbers that are greater than 0 and less than 10, non-inclusive:

{1, 2, 3, 4, 5, 6, 7, 8, 9}

Write in roster notation all integer numbers that are less than two, inclusive.

{..., −2, −1, 0, 1, 2}

Interval and Graphical Notation

An interval is a connected subset of numbers, an alternative to expressing the values as an inequality. When using interval notation we use two types of symbols:

" ( " which means non-inclusive or open.

" [ " which means inclusive or closed.

Here’s how you would describe a set with interval notation:

(a, b]

This set represents all numbers between a and b, including b but not including a.  In set-builder notation, this would be expressed as {x | a < x ≤ b}.

 

You can show an interval on a graph as well.  Here are six types of interval notation and how they generally look on a number line:

 

Notice how interval notation and graphical notation always include all numbers in their sets, not just the integers.  For example, 3.2 is an element of the set [2, 5], but not the set {2, 3, 4, 5}.

Example

Write this notation for all integers between 23 and 27 inclusive.

Roster Notation

{23, 24, 25, 26, 27}

Set-Builder Notation

{x ∈ ℤ | 23 ≤ x ≤ 27}

 

Write this notation for all numbers between 23, inclusive, and 28, non-inclusive.

Interval Notation

[23, 28)

Graphical Notation

 

Practice

1.  Express the set of positive multiples of 5 using roster notation.

2.  Express the set of numbers greater than 20 using set-builder notation.

3.  Express the set of numbers between 12, non-inclusive, and 16, inclusive.

4.  Express the set in Exercise 3 using a graph.

Answers

1.  {5, 10, 15, 20, 25, ...}

2.  {x | x > 20}

3.  (12, 16]

4.