Surface Area and Volume of Spheres
 Learning Target: I can compute the surface area and volume of a sphere.
Learning Target: I can compute the surface area and volume of a sphere.
Surface Area and Volume of Spheres
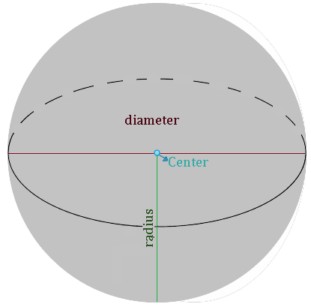
The diameter of the sphere is the straight line that connects two points on the sphere’s surface while passing through the center.
The radius of the sphere is a straight line from the center of the sphere to any point on the surface of the sphere.
The surface area of a sphere with radius r is
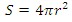
or using diameter
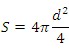
S = πd 2
A spherical ball is inflated to 4 times its original radius. If the original radius was 4 cm, would the surface area quadruple as well?
For the original sphere with a radius r, we can calculate the surface area:

The surface area of the inflated sphere is 16 times the surface area of the original, so it does NOT quadruple.
Taking a look at the image below, we can picture the interior of a sphere. Its radius r is approximated by n pyramids, each of them with a height equal to the radius of the sphere and a defined base.
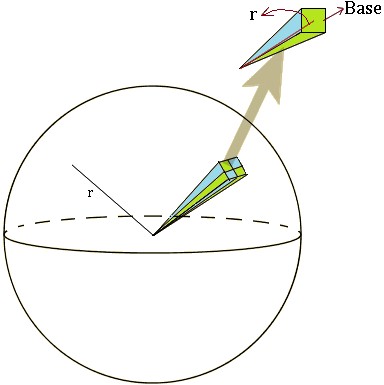
We can use this formula to find the volume of the pyramid:
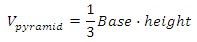
Since we have n amount of pyramids that represent the volume inside the sphere, the surface area for the sphere is defined as
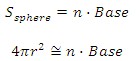
We can approximate the volume of the sphere by combining the equations adding all of the n pyramids inside the sphere. This gives us:
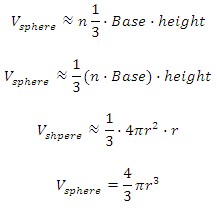
You are given a clay prism (see below) and are told to create a ball using all the clay. What will be the radius of the ball you create?
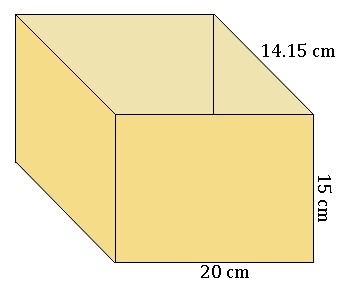
To find the volume of the prism we have
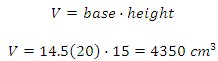
Since they clay ball and prism will have the same volume, we can use the volume formula for the sphere to find the radius.
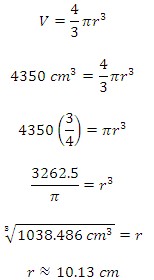
The radius of the ball is then approximately 10.1 centimeters.
Let's Practice Together
1.) A standard ping pong ball has a diameter of 40 millimeters. Find its surface area (to the nearest square millimeter) and volume (to the nearest cubic millimeter).
Your Turn
Round answers to the nearest hundredth.
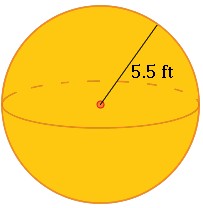
2.) Find the surface area:
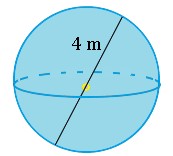
3.) Find the volume of the sphere below:
Check for Understanding
1.) If three small spheres each have a radius of 250 cm, and the large sphere has a surface area of 2,500 m2, how much of the volume of the big sphere is not occupied by the small spheres?
Answers
1. 5,027 mm2; 33,510 mm3
2. about 380 ft2
3. about 33.5 m3
Check for Understanding
1. about 11,560 m3