Volume of Prisms, Cylinders, Cones, and Pyramids
 Learning Target: I can compute the volume of various 3-D objects.
Learning Target: I can compute the volume of various 3-D objects.
Volume of Prisms, Cylinders, Cones, and Pyramids
The volume of a prism is the product of the area of the base and the height of the object:
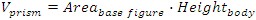
For example, the volume of a cube is
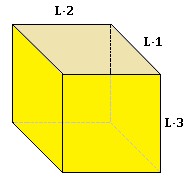
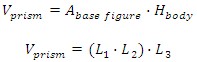
In a cube all the sides have the same length (L1 = L2 = L3), therefore
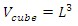
The box shown is 10 cm wide, 4 cm long, and 6 cm high. If you have gifts that are cubes, with a length of 1 cm, how many cubes will fit inside the box? What is the volume of the box?
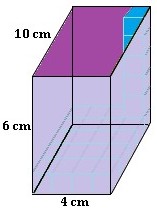
The base of the box is 4 cm by 10 cm. The face is a rectangle, and to find the area of a rectangle we have
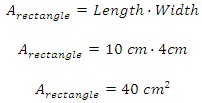
Since we know that our gifts are cubes of length 1 cm, we can find their volume as
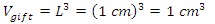
with a base area of
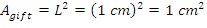
If we take the proportion of the areas of the base of our box and the gifts we can find how many cubes we can fit in the base area of the box:
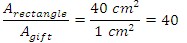
So we can fit 40 of the gift boxes per base area, but we need to find out how many gifts will fit in the whole box. Five more layers of cubes can be placed on top of the base layer to fill the box. Now that the box contains 6 layers of gifts, with 40 gifts on each layer, the box will be filled by a total of 240 gifts. For this example, we used the method for finding the volume of a prism to find how many 1 cm3 gift boxes can fit.
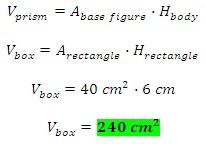
The volume of a cylinder follows the same logic as the prism. The only difference is a change in the base, which is now a circle. Then the volume of the cylinder is
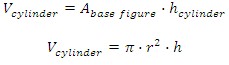
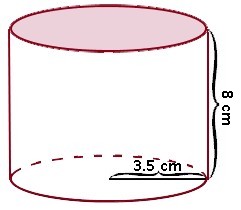
Find the volume of the following right circular cylinder.
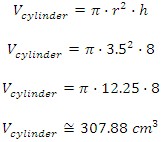
As we already saw, the volume of a prism is the area of the base times the height of the prism. The volume of the pyramid has the same base area and height as the prism, but with less volume than the prism. The volume of the pyramid is one third the volume of the prism.
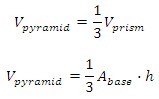
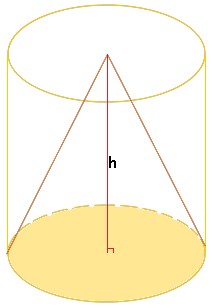
To find the volume of a cone, we follow the same principle as for the cylinder. So we use the same method, but the base is now circular. Then we have
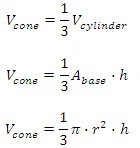
Let's Practice Together
1.) A cone has a diameter of 48 cm and a height of 60 cm. Find its volume to the nearest cubic centimeter.
For the following bodies, find the value for x. Round to the nearest tenth when necessary.
2.)
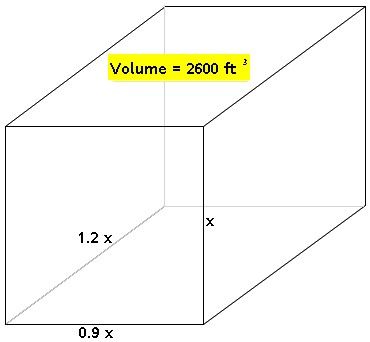
Your Turn
3.)
4.)
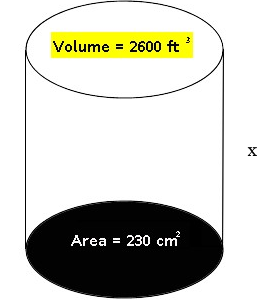
5.)
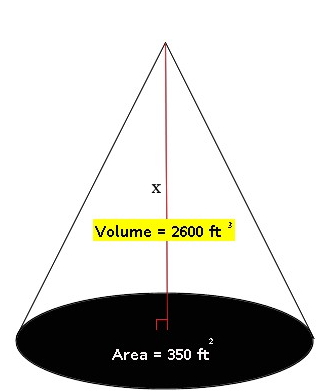
Check for Understanding
1.) The glass pyramid outside the Louvre Museum in Paris has a square base with a length of 35 meters, and a height of 21 meters. Find its volume in cubic meters.
Answers
1. 36,191 cubic cm
2. about 13.4
3. 13
4. about 11.3
5. about 22.3
Check for Understanding
1. 8,575 cubic meters