Polynomial Identities
When you multiply two binomials together, you use the FOIL method to find their product.
(x + 5)(x − 8) = x2 − 8x + 5x − 40 = x2 − 3x − 40
Sometimes, though, the binomials you're multiplying give you a shortcut for you to find the products more quickly. The results from these examples are known as polynomial identities. Some of the more famous examples are shown below.
1. Difference of squares
When you FOIL the binomials (a + b) and (a − b) together, look what happens to the middle terms:
(a + b)(a − b) = a2 − ab + ab − b2 = a2 − b2
This identity gives you the difference of squares. (a + b)(a − b) = a2 − b2
This expression is very commonplace in algebra, and may come in a variety of forms. When factoring an expression, be on the lookout for situations like this.
x2 − 36 = (x + 6)(x − 6)
5x2 − 20 = 5(x2 − 4) = 5(x + 2)(x − 2)
x4 − 81 = (x2 + 9)(x2 − 9) = (x2 + 9)(x + 3)(x − 3)
A Prime Number Property If you square any prime number greater than 3, the result will be one more than a multiple of 12. You can verify this interesting property with algebra. Let p be a prime number greater than 3. The property says that p2 is one more than a multiple of 12. In other words, the expression p2 − 1 has 12 as a factor. Let's use factoring to explore this further: p2 − 1 = (p + 1)(p − 1) All prime numbers greater than 3 are odd, so both p + 1 and p − 1 are even, meaning that they both have 2 as a factor. Their product must then have 2 × 2 = 4 as a factor. Also, given any three consecutive numbers-- p − 1, p, and p + 1 in this case-- one of them has to be a multiple of 3. A prime number can't have 3 as a factor, so that means either p − 1 or p + 1 has 3 as a factor. Therefore, the product (p + 1)(p − 1) has 3 as a factor, and therefore p2 − 1 has 4 × 3 = 12 as a factor. |
2. Binomial squares
When you square a number, you multiply it by itself, as in 52 = 5 × 5 = 25. Binomials are no different. If you have to expand (a + b)2, you do that by multiplying (a + b) by (a + b). You do NOT do that by distributing the exponent over the added terms; rather, you use the FOIL method.
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
Looking at a and b as generic placeholders, you can see that squaring (a + b) gives an expression with three terms: The square of the first, twice the product of the two, and the square of the second. If you can remember that for any two-term expression being squared, it will make the work a lot easier.
(4x + 5y)2 = (4x)2 + 2(4x)(5y) + (5y)2 = 16x2 + 40xy + 25y2
This also works when you square (a − b). The only difference is that the middle term (and not the last term) gets subtracted.
(a − b)2 = a2 − ab − ab + b2 = a2 − 2ab + b2
(3p − q2)2 = (3p)2 − 2(3p)(q2) + (q2)2 = 9p2 − 6pq2 + q4
The Pythagorean Theorem The lengths of the three sides of a right triangle have a famous relationship: a2 + b2 = c2, where a and b are the lengths of the legs and c is the length of the hypotenuse. A squared binomial can be used to prove this. If we place a point on each side of a square, dividing it into a length of a and a length of b as shown below, the square will have a side length of a + b. 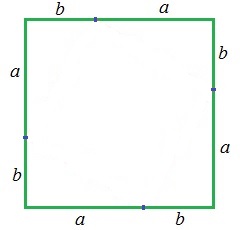
The area of this square is (a + b)2 = a2 + 2ab + b2. Now if we connect the four points on the square sides as shown, we create a smaller square with a side length of c, as well as four right triangles. 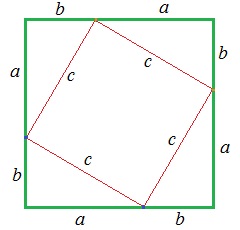
The area of the smaller square is c2, and each of the four triangles has area 1/2ab. Together, the triangles have area 4 × (1/2ab) = 2ab. The area of the whole figure can now be expressed as c2 + 2ab. Setting the two expressions equal to each other, we have a2 + 2ab + b2 = c2 + 2ab. You can see how subtracting the 2ab from both sides produces the equation a2 + b2 = c2. |
3. Sum and difference of cubes
When two cubed expressions are being added or subtracted together, the expression also factors into a distinctive pattern.
a3 + b3 = (a + b)(a2 − ab + b2)
a3 − b3 = (a − b)(a2 + ab + b2)
If the expressions confuse you, just remember that the sign in the middle of the original expression is the same sign found in the middle of the first factor. The sign in front of the ab term in the second factor is the opposite, and b2 is always positive. The trinomial second factor that results from this is always prime, so don't bother trying to factor that one.
Just like with the difference of squares, the sum or difference of cubes can be hidden within more detailed expressions:
3x3 + 375 = 3(x3 + 125) = 3(x3 + 53) = 3(x + 5)(x2 − 5x + 25)
x6 − 64 = (x2)3 − 43 = (x2 − 4)(x4 + 4x2 + 16) = (x + 2)(x − 2)(x4 + 4x2 + 16)
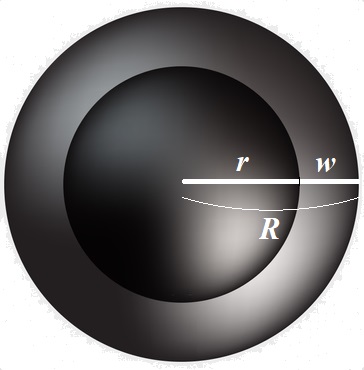
Insulating a Sphere If you place a small sphere inside a larger sphere with the intention of filling the space between them with insulation, you can find the amount of space by subtracting the spheres' volumes. If R is the radius of the large sphere and r is the radius of the smaller sphere, this gives us:
Factoring out the common , you're left with the difference of cubes R3 − r3. You can use the factoring method to get a new expression for the insulation's volume.
The difference between the radii, R − r, is a factor of the expression. If you want, you can replace that with a single variable, say w, and make a simpler formula that eliminates the need for subtraction.
|
Practice
A complex number is a number in the form a + bi, where i2 = -1. You can multiply complex numbers using the FOIL method:
(3 + 5i)(2 − 7i) = 6 − 21i + 10i − 35i2
= 6 − 11i − 35(-1) = 41 − 11i
Perform the following operations.
1. (4 + 9i)2
2. (8 − 3i)2
You can divide complex numbers through algebraic methods. Express the division in fraction form, and multiply both numbers by the denominator's conjugate. A conjugate of a complex number is the same number but with the opposite sign in the middle.
Divide (3 + 5i) ÷ (2 − 7i).
Notice how this tactic creates the difference of squares in the denominator, eliminating the middle term and making the denominator a real number.
Perform the following divisions.
3. (1 − 4i) ÷ (5 + 6i)
4. (9 − 2i) ÷ (3 − 8i)
Answers
1. -65 + 72i
2. 55 − 48i
3.
4.


