 Learning Target: I can write a linear equation based on given data and use it to solve problems.
Learning Target: I can write a linear equation based on given data and use it to solve problems. Learning Target: I can write a linear equation based on given data and use it to solve problems.
Learning Target: I can write a linear equation based on given data and use it to solve problems.
Constructing Functions
A function is a rule that establishes a relationship between two quantities, called the input and the output. Functions can be described in an input-output table.
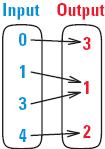
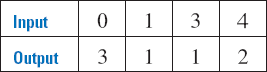
Example 1
The diagram below shows the first six triangular numbers, 1, 3, 6, 10, 15, 21, which continue on following the same pattern.
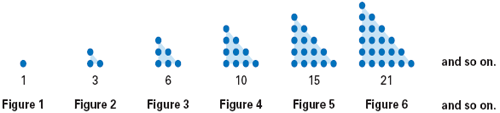
a.) Make an input-output table in which the input is the Figure number n and the output is the corresponding triangular number T.
b.) Does the table represent a function? Justify your answer.
c.) Describe the domain and range.
a.)

b.) Yes, because for each input there is exactly one output.
c.) The collection of all input values is the domain: 1, 2, 3, 4, 5, 6, . . . . The collection of all the output values is the range: 1, 3, 6, 10, 15, 21, . . . .
Example 2
As you dive deeper and deeper into the ocean, the pressure of the water on your body steadily increases. The pressure at the surface of the water is 14.7 pounds per square inch (psi). The pressure increases at a rate of 0.445 psi for each foot you descend. Represent the pressure P as a function of the depth d for every 20 feet you descend until you read a depth of 120 feet.
a.) Write an equation for the function.
b.) Create an input-output table for the function.
c.) Make a line graph of the function.
a.) To write an equation for the function, apply the problem solving strategy. Write a verbal model, assign labels, and write an algebraic model.
| Verbal model | 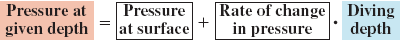 |
Labels | Pressure at given depth = 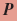 (psi) (psi)Pressure at surface = 14.7 (psi) Rate of change in pressure = 0.445 (psi per foot of depth) Diving depth = 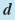 (feet) (feet) |
Algebraic model | 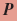 = 14.7 + 0.445 = 14.7 + 0.445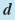 where 0 ≤ where 0 ≤ 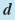 ≤ 120 ≤ 120 |
b.) Use the equation to make an input-output table for the function. For inputs, use the depths for every 20 feet you descend down to 120 feet.
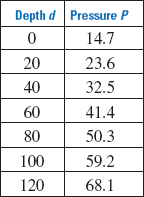
c.) You can represent the data in the table with a line graph.
Let's Practice Together
The fastest winning speed in the Daytona 500 is about 178 miles per hour. Calculate the distance traveled d (in miles) after time t (in hours) using the equation d = 178t. (Source: NASCAR)
1.) Complete the input-output table.

2.) Describe the domain and the range of the function whose values are shown in the table.
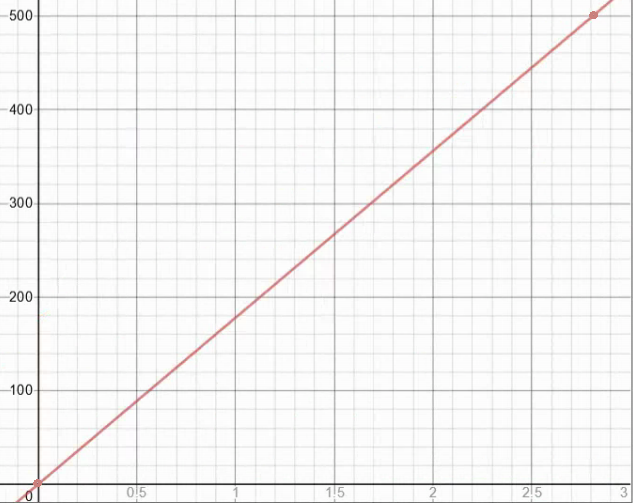
3.) Graph the data in the table. Use this graph and the fact that when t = 0, d = 0 and when t = 2.81, d = 500 to graph the function.
Your Turn
A drive-in movie theater charges $5 admission per car and $1.25 for each person in the car. The total cost C at the drive-in movie theater is given by C = 5 + 1.25n, where n represents the number of people in the car. (Assume a maximum of 7 people per car.)
4.) Make an input-output table for the function.
5.) Describe the domain and range of the function whose values are shown in the table.
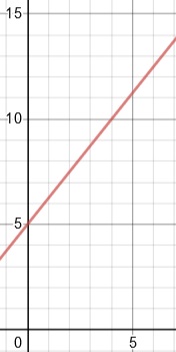
6.) Graph the data shown in the input-output table.
You start a portable ice cream stand. Your specialty is a banana split that costs $1.10 to prepare. Suppose you are working on the pier by the Pacific Ocean and selling each banana split for $2.50.
7.) Write a function that gives the profit you expect from working on the pier.
8.) You must spend $75 on equipment and supplies for your stand. Write a function for the profit that includes this cost.
9.) Use your equation from exercise 8 to find the profit you will earn if you sell 95 banana splits.
10.) Use your equation from exercise 8 to find out how many banana splits you must sell to have a profit of $170.
Check for Understanding
1.) Leann runs a tutoring business. She charges a one-time $20 admission fee and $15 per hour for each session. Write a function that gives the cost (C) of a session in terms of the hours (h). Find the cost of a 3-hour session.
Answers
1. 44.5, 89, 133.5, 178, 222.5, 267
2. Domain: {0.25, 0.50, 0.75, 1.00, 1.25, 1.50}, Range: {44.5, 89, 133.5, 178, 222.5, 267}
3.
4.
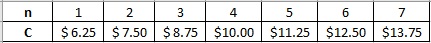
5. Domain: {1, 2, 3, 4, 5, 6, 7}, Range: {$6.25, $7.50, $8.75, $10.00, $11.25, $12.50, $13.75}
6.
7. P = (2.50 − 1.10)b = 1.40b
8. P = 1.40b − 75
9. $58
10. 175
Check for Understanding
1. C = 15h + 20; $65