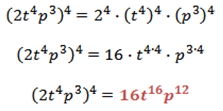Monomials
Monomials and the GCF
A monomial is a number, a variable raised to a whole number, or a product of a number and one or more variables.
Examples: 12x2y, 3mn, 64w3y2
In algebra, a polynomial is the sum of two or more monomials.
Examples: (12x2y2 + 3x3y2); (12m + 64); and (3p − 64p3q + 12pq2)
A polynomial with 2 terms is known as a binomial, and it's the sum of two monomials. A polynomial with 3 terms is known as a trinomial, and so on.
Factoring Monomials
To factor a monomial means to write the monomial as a product of its factors.
Finding the greatest common factor (GCF)

Power of a Power Property
To raise a monomial to a power, multiply exponents for each variable by the external power; and raise each numeric factor to the external power.
Example:
Simplify: (2t 4p3)4
Practice
Simplify the following monomials.
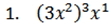
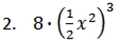
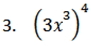
Find the GCF for the following.
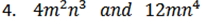
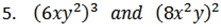
Answers
1.) 27x7
2.) x6
3.) 81x12
4.) 4mn3
5.) 8x3y2