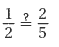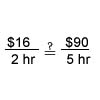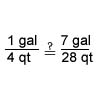Solve Proportions
Solve Proportions
True Proportions
- A proportion is an expression of the equality of two ratios or rates.
- A proportion is true if the fractions are equal when written in lowest terms.
Example
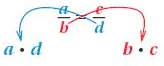
In a true proportion, ad = bc.
For example, the equation below
is a true proportion because 3 × 12 = 4 × 9.
Solving Proportions
Sometimes one of the numbers in a proportion is unknown. In this case, it is necessary to solve the proportion.
To solve the proportion, find a number to replace the unknown so that the proportion is true. You can use cross-products to solve a proportion.
Example
Find n on the following proportion
Solution
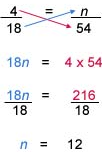
Practice
1.) Use cross products to determine whether each equation given below is a true proportion.
a.)
b.)
c.)
d.)
2.) Solve each proportion. Round to the nearest hundredth if needed.
a.)
b.)
c.)
d.)
e.)
3.) Solve the following problems using a proportion.
a.) The dosage of a certain medication is 2 ounces for every 50 pounds of body weight. How many ounces of medication are required for a person who weighs 175 pounds?
b.) Three tablespoons of fertilizer are added to every 4 gallons of water. How many tablespoons of fertilizer are required for 10 gallons of water?
c.) The scale on a map is 1.25 inches equals 10 miles. How far apart in miles are two towns that are 2 inches apart on the map?
d.) A contractor charges $9.25 per square foot for stucco work. A homeowner was given the estimate of $5,550 for stucco work on her home. What was the square footage used for the estimate?
Answers
1.)
a.) not true
b.) not true
c.) not true
d.) true
2.)
a.) n = 8
b.) w = 9
c.) t = 16
d.) a = 6
e.) d = 7
3.)
a.) 7
b.) 7.5
c.) 16 miles
d.) 600