Slope-Intercept Form
When graphing a line, it is often helpful to write the equation in slope-intercept form, y = mx + b, where m is the slope of the line, and b is the y-intercept.
The slope of a line may also be determined when two points on the line are known. The slope is calculated as the change in the y values over the change in the x values.
Linear inequalities may be graphed in the same way as lines. Graph the equation as if it had an equal sign. Use a dashed line for < or >. Use a solid line for < or >. Test a point not on the line to check whether it is a solution of the inequality. If the test point is a solution, shade its region. If the test point is not a solution, shade the other region.
Practice
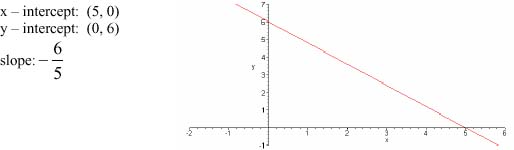
1. Find the x and y-intercepts, slope and graph of 6x + 5y = 30.
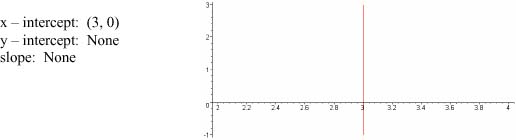
2. Find the x and y-intercepts, slope and graph of x = 3.
3. Find the x and y-intercepts, slope and graph of y = -4.
4. Write in slope-intercept form the line that passes through the points (4, 6) and (-4, 2).
5. Write in slope-intercept form the line perpendicular to the graph of 4x - y = -1 and containing the point (2, 3).
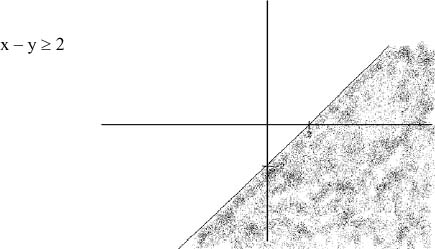
6. Graph the solution set of x - y > 2.
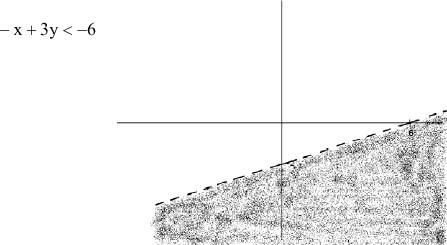
7. Graph the solution set of -x + 3y < - 6.
Answer Key
1.
2.
3.
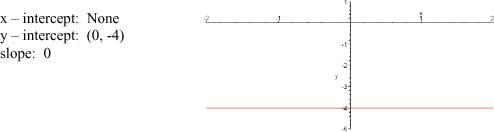
4. 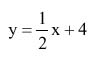
5. 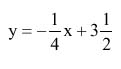
6.
7.