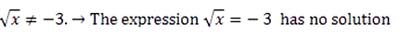Solve Radical Equations
Solve Radical Equations
A radical equation is an equation in which at least one variable expression is under a root sign.
The most common type of radical equation involves square roots, but cube roots or other roots are also radical expressions.
Examples
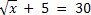 is a radical equation.
is a radical equation.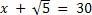 contains a radical expression, but for the purposes of this lesson, is not considered a "radical equation."
contains a radical expression, but for the purposes of this lesson, is not considered a "radical equation."Solving Radical Equations
As with other linear equations, the objective is to isolate the variable. To accomplish this, apply inverse operations as needed.
The inverse operation of a square root is to square. (Similarly, the inverse of a cube root is to cube, or raise to the power of three, and so forth.)
Example

Square Sides not Terms
Recall that when working with equations, any operation you perform on one side of the equality sign must also be performed on the other side to keep the values equal. When squaring both sides, be careful that you square sides, not terms. Exponents do not "distribute" across addition.
Example
Solve:
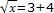
x = (3 + 4)2 do not square individual terms -- x 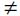 32 + 42
32 + 42
x = (7)2 x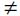 9 + 16
9 + 16
x = 49 x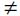 25
25
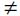 32 + 42
32 + 42x = (7)2 x
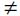 9 + 16
9 + 16x = 49 x
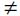 25
25Principal Square Root
The principal square root of a number is a positive number, even though its opposite number, which is negative, can also be the square root. For example, the principal square root of 16 is 4, although both -4 and 4 are square roots of 16.
Obtaining Results that are Real Numbers
It is important to note that a positive square root can never equal a negative number. This is because any real number times itself will yield a positive number.
Example
Checking Answers
Make sure to check all possible answers to radical equations because you may have found some false solutions: When squaring two sides of an equation, the resulting equation is not always equivalent to the original.
Example
Solve:
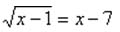
Solve:
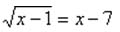

Check answers to ensure that results are real numbers.
Substitute the values found for x into the original equation.
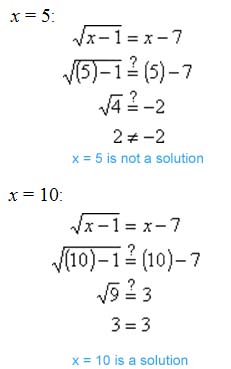
The only solution to this equation is x = 10.