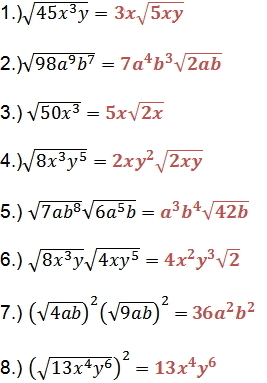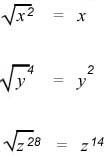Simplify Square Roots
Simplify Square Roots
To simplify square roots, we can make use of the product rule for square roots, which states that the product of two square roots is equal to the square root of the product for all real numbers.
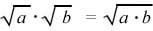
To Simplify the Square Root of a Constant:
1) Write the constant as a product of the largest perfect square factor and another factor.
2) Use the product rule to write the expression as a product of square roots, with each square root containing one of the factors.
3) Find the square root of the perfect square factor.
Examples:
To Simplify Square Roots Containing Variables:
1) If the expression consists of a variable raised to an even power, the square root of the expression equals the variable raised to one-half of that power.
Examples:
2) If the variable contains an odd power, express it as the product of two factors, one having an exponent 1 and the other with an even exponent.
3) Use the product rule to simplify.
Examples:
Practice
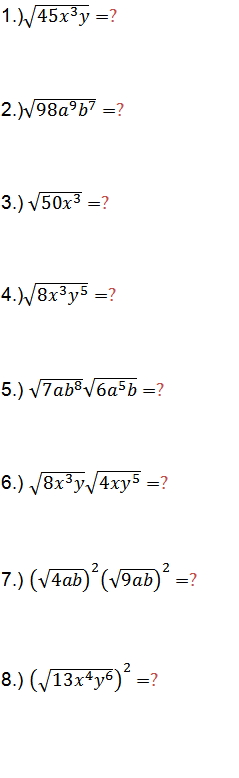
Answer Key