Multiplication and Division with Decimals
Multiplication and Division with Decimals
Multiplication with Decimals
Decimals are multiplied as if they were whole numbers, and then the decimal point is placed in the product.
0.7  0.352 = 2464 (now you need to place the decimal point in the product)
0.352 = 2464 (now you need to place the decimal point in the product)
To find out where the decimal point should be placed, count the number of decimal places after the decimal point in each factor.
0.7 1 decimal place
0.352 3 decimal places
A total of 4 decimal places
Once you have found the sum of the decimal places in each factor, you know how many decimal places the product will need after its decimal point. Starting at the far right of the number, move the decimal point toward the left that number of decimal places.
0.2464 (4 decimal places after the decimal point)
Example
Solve: 0.9 × 0.3
Solution
First multiply ignoring the decimal points
3 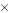 9 = 27
9 = 27
Then place the point in the product (in this case, two decimal places)
27 => 0.27
0.3 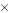 0.9 = 0.27
0.9 = 0.27
If necessary, add zeros to the left side of the product.
Example(2)
Solve: 0.05 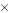 0.4
0.4
Solution
Multiply as you would whole numbers, ignore decimal places
0.05
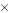 0.4
0.4
20
Count the number of decimal places needed for the product
0.05 2 decimal places
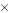 0.4 1 decimal place
0.4 1 decimal place
20 A total of 3 decimal places
Write zeroes in front of the whole number to place the decimal point correctly
0.05
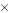 0.4
0.4
0.020
Therefore 0.05 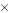 0.4 = 0.02
0.4 = 0.02
Dividing Decimals
1. Move the decimal point in the divisor to the right to make the divisor a whole number.
2. Move the decimal point in the dividend the same number of places to the right.
3. Place the decimal point in the quotient directly over the decimal point in the dividend for the final quotient.
4. Divide as if working with whole numbers
At times, it may be necessary to round a quotient to a given place value.
Example
Solve and round to the nearest hundredth: 1.5 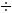 0.45
0.45
Since 3 < 5, rounding the answer we obtain: 1.5 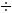 0.45 = 3.33
0.45 = 3.33
Decimals with Exponents
A decimal with exponents is simply the decimal multiplied by itself n times, where n is the value for the exponent.
Example
Evaluate the following expressions.
1.) (0.6)2 = 0.6 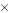 0.6 = 0.36
0.6 = 0.36
2.) (0.6)3 = 0.6 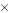 0.6
0.6 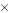 0.6 = 0.36
0.6 = 0.36 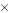 0.6 = 0.216
0.6 = 0.216