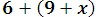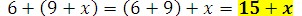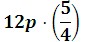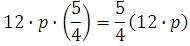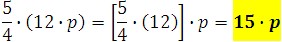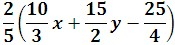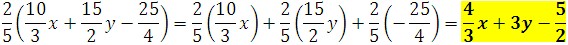Properties of Real Numbers
Properties of Real Numbers
Real Numbers include many sets of numbers: integers, fractions, decimals, rational numbers, and irrational numbers. The one set of numbers that is not in this group is "imaginary numbers."
For all real numbers x, y, and z, the following properties apply:
Closure Properties
The sum or product of two real numbers is a real number.
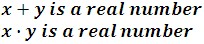
Commutative Properties
The sum or product of two real numbers is the same regardless of their order.
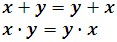
Identity Properties
The sum of a real number and 0 is that real number.
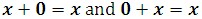
The product of a real number and 1 is that real number.
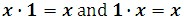
Inverse Properties
The sum of any real number and its opposite is 0.
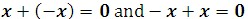
The product of any nonzero real number and its reciprocal is 1.
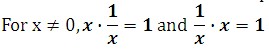
Associative Properties
The sum or product of three real numbers is the same no matter which two are added or multiplied first.
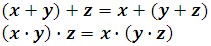
Distributive Property
When a real number gets multiplied by the sum or difference of real numbers, it gets multiplied by every number within the sum or difference.
x(y + z) = xy + xz
x(y - z) = xy - xz
Careful! Notice the difference between the associative and commutative properties.
- For the associative properties, the order of the numbers does not change, but their grouping does.
- For the commutative properties, the order of the numbers does change from one side of the equal sign to the other.
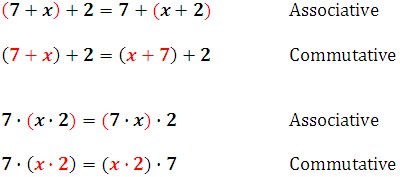
Examples
1. Simplify the following expression.
Using the associative property, we can simplify it.
2. Simplify the following expression:
First, let us use the commutative property.
Now we'll use the associative property.
3. Use the distributive property to rewrite the following expression:
4. Use the distributive property to factor the following expression:
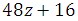
= 16(3z + 1)