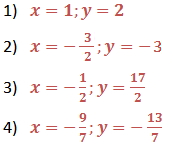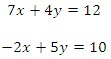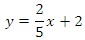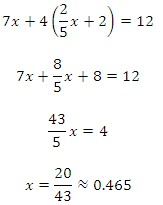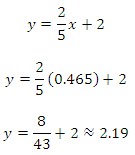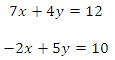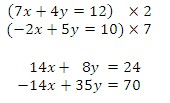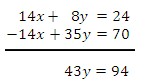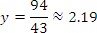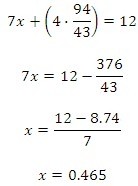Solve Linear Systems
Solving Linear Systems
A set of equations is identified as a system of equations. The answer to a system of equations must satisfy all equations in the system. If all equations in a system are linear, the system is a linear system. The answer to a system of linear equations in two variables is an ordered pair [i.e. (x, y)] that satisfies each equation in the system.
There are three common ways to solve linear systems:
1. Solving by Graphing
2. Solving by Substitution Method
3. Solving by Linear Combinations
1. Solving by Graphing
Because the solution of a linear system satisfies each equation in the system, the solution must lie on the graph of both equations. When the solution has integer values, it is possible to find the solution by graphical methods. To solve a linear equation by graphing we use the following steps:
- Write each equation in a form that is easy to graph(i.e., slope-intercept form).
- Graph both equations in the same coordinate plane.
- Estimate the coordinates of the point of intersection.
- Check the coordinates algebraically by substituting them into each equation of the original linear system.
Example
Use the graph to solve the system of linear equations.
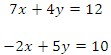
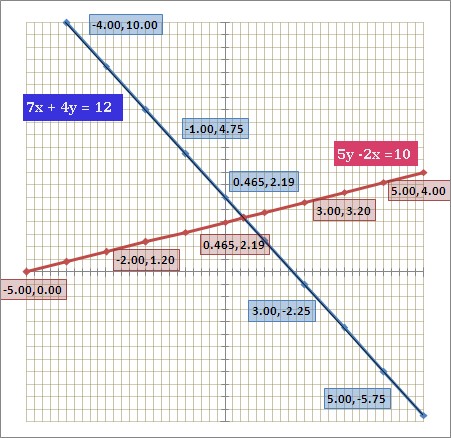
The graph gives us a visual model of the solution. Looking at the values for each graph, we can see that the lines intersect at (0.465, 2.19). To check the solution we can substitute the values for x and y in each equation.
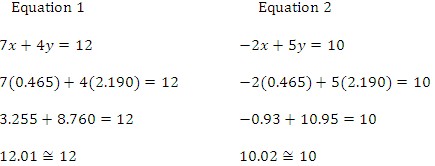
Because the lines in the graph of this system intersect at only one point, the coordinate pair, (0.465, 2.19), is the only solution to this linear system.
2. Solving by Substitution Method
In a system with two variables, the substitution method involves using one equation to find an expression for one variable in terms of the other and then substituting that solution into the other equation of the system. These are the steps to follow when using substitution:
- Solve one of the equations for one of its variables.
- Replace the expression from the previous step into the other equation, and solve for the other variable.
- Substitute the value from the previous step into the adjusted equation from the first step and solve.
- Check the solution in each of the original equations.
Example
Solve the following linear system by using the substitution method:
a.) Solve for y in equation 2.
b.) Substitute the value for y in equation 1 and solve.
c.) Substitute the value of x into the revised equation 2:
d.) Check that (0.465, 2.19) is a solution by substituting the values of x and y into each of the original equations.
3. Solving by Linear Combinations
A linear combination of two equations is an equation attained by adding one of the equations or a multiple of one of the equations to the other equation. These are the steps to follow when using combinations:
- Arrange the equations with like terms in columns.
- Multiply one or both of the equations by a number to obtain coefficients that are equal and opposites for one of the variables.
- Add the equations from the previous step. Combining like terms will eliminate one variable, so you can solve for the remaining variable.
- Substitute the value obtained on the previous step into either of the original equations and solve for the variable.
- Check the solution in each of the original equations.
Example
Solve the following linear system using the method of linear combinations.
a.) Arrange the equations.
For this example they are already arranged.
b.) Multiply the first equation by 2 and the second equation by 7, so that the coefficients for x are equal and opposites.
c.) Add the equations to get an equation in one variable.
d.) Substitute the value of y in the first equation and solve for x.
e.) Check that (0.465, 2.19) is a solution by substituting the values of x and y into each of the original equations.
Guided Practice
Solve the following linear systems by using substitution.
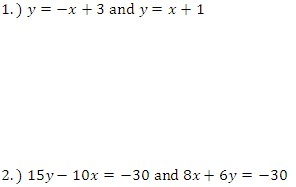
Solve the following linear systems by using linear combinations.
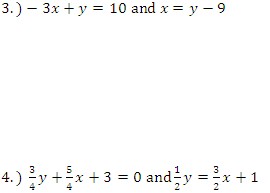
Answer Key