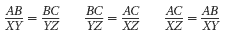Similar Polygons

               

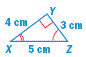
ΔABC ~ ΔXYZ

Corresponding angles are congruent.

∠A ≅ ∠X

∠B ≅ ∠Y

∠C ≅ ∠Z

Corresponding side lengths are proportional.

Identifying Similar Polygons

Example

Are these television screens similar?

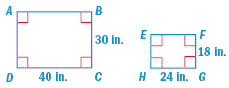
Step 1 Corresponding angles are congruent.  Each angle measures 90^o.

∠A ≅ ∠E,   ∠B ≅ ∠F,   ∠C ≅ ∠G,   ∠D ≅ ∠H

Step 2 Corresponding side lengths are proportional.

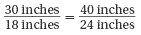
30 x 24 = 18 x 40

720 = 720

Therefore, Quadrilateral ABCD ~ Quadrilateral EFGH.  The television screens are similar.

Using Similar Triangles

Example

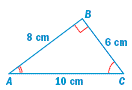
In the diagram, ΔKLM ~ ΔNPQ. Find the value of y.

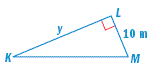
Corresponding side lengths are proportional.

The value of y is 24 meters.

Practice

1.  Find the value of x.

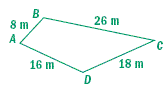
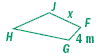
Quadrilateral ABCD ~ Quadrilateral FGHJ

CJ is 5 feet tall and casts a 7-foot shadow.  At the same time, a tree casts a 14-foot shadow.  The triangles formed are similar. Find the height of the tree.

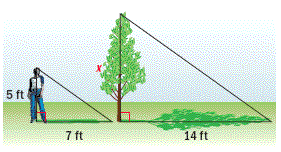
Solution

You can use a proportion to find the height of the tree.

Step 1   Write a proportion.

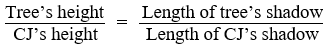
Step 2   Substitute given values.

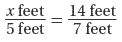
Step 3   Solve the proportion.

x = 10

The tree is 10 feet tall.

Dilations

A dilation stretches or shrinks a figure.  The image created by a dilation is similar to the original figure.  The scale factor of a dilation is the ratio of corresponding side lengths.  In this course, the center of dilation will always be the origin.

Dilation
To dilate a polygon, multiply the coordinates of each vertex by the scale factor k and connect the vertices.

Rule:  P(x, y) --> P'(kx, ky)
Example:  P(4, 1) --> P'(8, 2)

---

 

Dilating a Polygon

Quadrilateral ABCD has vertices A(-1, -1), B(0, 1), C(2, 2), and D(3, 0).  Dilate using a scale factor of 3.

Solution 

Step 1   Find the vertices of the image.

    

Step 2   Graph the image of the quadrilateral.

---

 

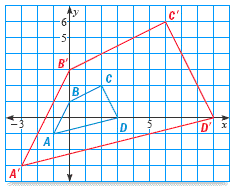
Practice

Graph the polygon with the given vertices. Then graph its image after dilation by the scale factor k.

2.  Triangle RST has vertices R(1, 1), S(3, 2), and T(2, 3); k = 2.

---

Graph the polygon with the given vertices. Then graph its image after dilation by the scale factor k.

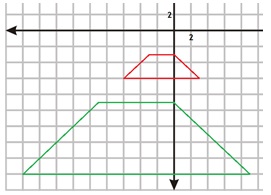
3.  Quadrilateral CDGH has vertices C(-6, -6), D(-3, -3), G(0, -3), and H(3, -6); k = 3

---

 

4.  Tommy is 5 feet tall and casts a 3-foot shadow. At the same time, a flagpole casts a 15-foot shadow.  What mathematical idea can Tommy use to find the height of the flag pole?

A inequality 
B congruence 
C similarity 
D symmetry

---

 

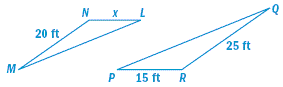
5.  ΔLMN is similar to ΔPQR. Find the value of x.

---

 

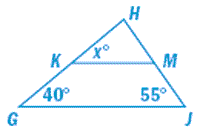
6.  Use the similar triangles to find the value of x.

ΔGHJ ~ ΔKHM

---

 

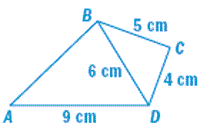
7.  Find the length of AB if ΔABD ~ ΔBCD.

A  6 cm 
B  7.2 cm 
C  7.5 cm 
D  11.25 cm

Answers

1. 8 m 
2. 
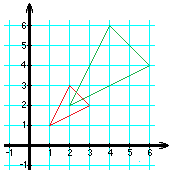
3. 
4. C 
5. 12 ft 
6. 40^o 
7. C